Propensity-score matching

There’s one more matching method to discuss. This matching method is called propensity score matching.

To begin, let’s see what a propensity score is. A propensity score is the probability that a subject will receive the treatment given the value of their covariates. If a subject’s propensity score is 0.8, that means that given the covariate values for the subject, there is an 80 percent chance that they would have been placed in the treatment group. It’s important to realize that the propensity score is different than the observed treatment status. Even if a subject’s propensity score is 0.8, we may observe that the subject is in the control group.

In fact, this is the nature of observational studies; propensity scores do not necessarily reflect the treatment status.

Things are a bit different in randomized experiments. In a randomized experiment, each subject’s propensity score is usually estimated at close to 0.5 because of the covariates’ natural balance. Every subject should have close to a 50 percent chance of being in the treatment or the control group.

Propensity-score matching was introduced in a 1993 paper by Rosenbaum and Rubin. In it, they argued that if a group of treated subjects has the same propensity score as a group of control subjects, then the distribution of covariates in each group must be the same. In other words, the propensity score is used as a combined index representing all covariates. So if we match on propensity scores, we’re in a way matching on all covariates.

In other words if $\text{PS}_i$ is the propensity score for subject $i$ in a sample,

P(X=x \text{ | } \text{PS}(X)=p, D=1) = P(X=x \text{ | } \text{PS}(X)=p, D=0)

where

\text{PS} = P(D=1 \text{ | } X)

This is a pretty useful finding. It means that instead of calculating distances and finding matches using all of our covariates, we can match on a single propensity score that represents the distribution of all relevant covariates.

Each group of observations with similar propensity scores forms a mini randomized experiment, and within each group, we can easily estimate the causal effect. Note that within each group, we don’t have to control for the covariates we matched on. In other words, the treatment and the covariates are independent within each propensity-score group.

X \perp D \text{ | } \text{PS}(X)

The equation above states the same thing we said above; In a subsample of matched treatment and control observations with similar propensity scores, all observations have the same distribution of the covariates regardless of their treatment status.

In the figure above, because all of the treatment and control observations in each group have the same propensity score, we can assume they have the same distribution of all observed covariates, just like in a randomized experiment.

A randomized experiment can be viewed as a special case of a matched sample. In a randomized experiment, there is a single group of observations, and every observation within it has the same propensity score of 0.5. Hence, all observations fall in the same group. The big difference between randomized experiment data and matched observational data is that in randomized experiments matching is naturally done on all observed and unobserved covariates, whereas, in an observational study, we can only match on observed covariates and not the ones we don’t observe 🙈

How to estimate propensity scores?

Let’s see how we estimate the propensity score. First, as we just learned, the propensity score is an indicator of the probability of receiving the treatment. Therefore, to estimate the propensity score for each subject, we use information about that subject.

One easy way of estimating propensity score is to regress the actual treatment variable on the covariates using logistic regression (because the left-hand side of the regression is binary). After that, we find the predicted values (fitted values) of the treatment status and this will be our propensity scores vector. Because it’s a vector, we have a propensity score for each subject.

Instead of logistic regression, we could also use any other predictive method such as machine learning algorithms. Since we only care about the predicted values, the coefficients of the logistic regression don’t matter. Also, we don’t have to be worried about the functional form of the regression (including interaction terms, quadratic or cubic terms, etc.).

As we said, the estimated propensity scores may not be correlated with the observed treatment status. For instance, for an observation in the treatment group ( $D_i=1$ ), we may estimate a propensity score of 0.1. This propensity score indicates that regardless of the treatment status, given the value of the covariates for that person, the chances that the person receives the treatment is 10 percent.

How do we match using propensity scores?

After estimating the propensity scores, we first check to see if the distributions of the propensity scores for the treatment and the control groups overlap. We can do this with a simple histogram or density plot. In general, there should be some overlap to satisfy the positivity assumption. But why?

As we saw in Module 2 on potential outcomes, the positivity assumption ensures that every subject in the study has some chance of receiving the treatment and the treatment assignment is not deterministic.

If the distribution of the propensity score for the treatment and the control groups don’t overlap, the positivity assumption is likely violated. Any causal effect estimated in the matched sample only applies to the observations in the overlapped region. We’ll only extrapolate for the causal effect of observations that lie outside the red region.

In a case like this, one potential approach is to limit the sample to observations that have a propensity score that lies in the overlapping (red) region. By doing this, we can have a better estimate of the causal effect of the treatment on the outcome. However, because our new sample is very different from the original population, the estimate does not tell much about the causal effect in the broader population.

Once we estimate the propensity scores, similar to the Mahalanobis distance method, we can find the distance between the propensity scores of the observations in the treatment group and the propensity scores of the observations in the control group. We can then use one-to-one or many-to-one matching to find the best matches for each observation in the treatment group, and we can use greedy or optimal matching to assign the matches.

Like we’ve seen with all other matching methods, you would use a caliper to exclude really bad matches. A rule of thumb typically used to identify good matches is this: if the distance between the propensity scores is smaller than 0.2 times the standard deviation of the propensity score, it’s a match made in heaven 😇

Ideally, covariates that were used in matching become balanced after we match subjects. And if that’s the case, these covariates could no longer be the cause of the difference in the treatment and control groups’ outcomes. Later, we will see that this is not always the case, and propensity-score matching doesn’t always lead to better (less biased) causal estimates.

An example: Heart disease and obesity

We are going to see how matching based on propensity score works empirically.

Let’s go over a fictional medical example in which we’re interested in the effect of obesity on the likelihood of having heart disease. The treatment variable is binary: it takes the value of 1 if the subject is obese, and it takes the value of 0 if the subject isn’t obese.

Let’s assume we’ve already identified that we need to control for age and diabetes to block all backdoor paths. The data is shown in the table below (note that these figures are made up, so you don’t have to give too much thought to them).

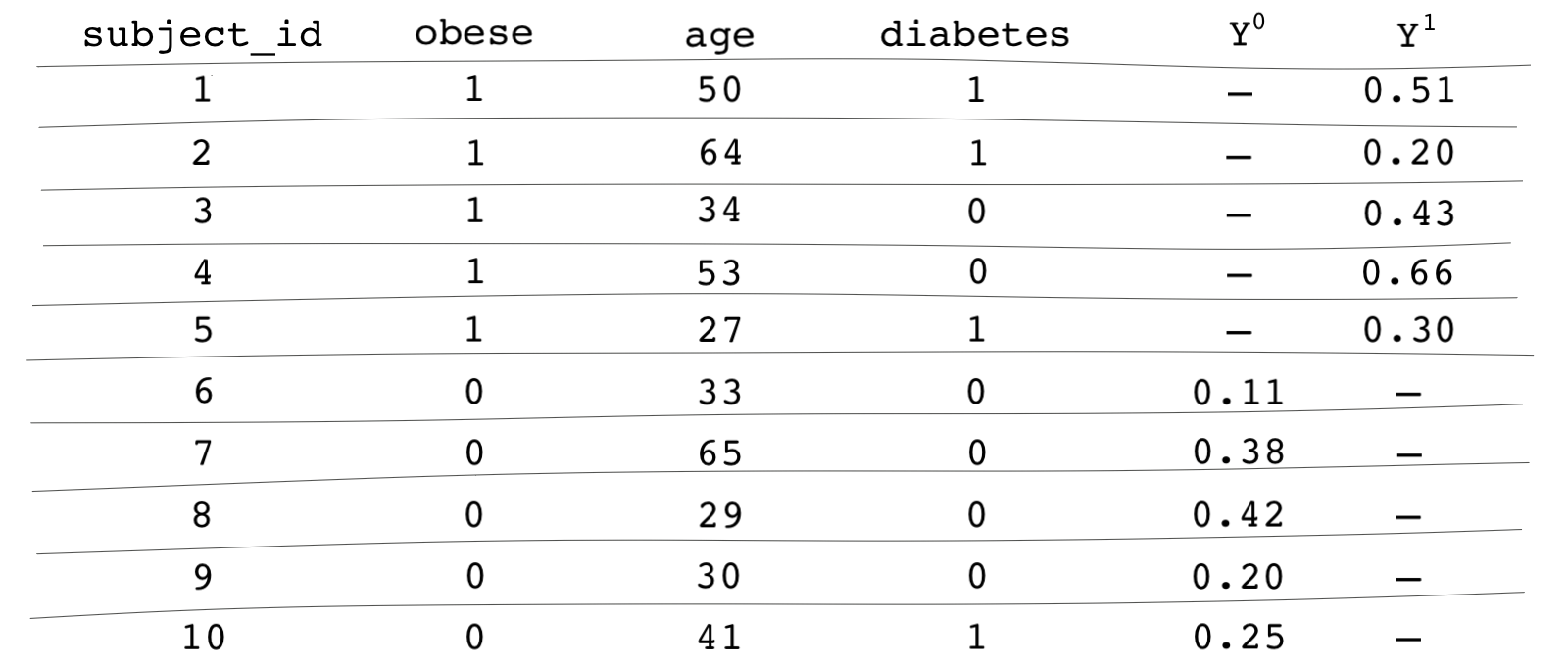
Columns $Y^0$ and $Y^1$ show the potential outcomes. Subject 1 is in the treated group, and therefore, we only potential outcome we observe is $Y^1$ . For Subject 1, the obesity variable and the diabetes variable take the value of 1 indicating that the subject is obese and has diabetes. Subject 6 is in the control group, so we only observe the potential outcome for $Y^0$ for this subject. We can see that subject 6 is not obese and does not have diabetes.

Which of the following statements is NOT true about Subject 10?

The subject has no chance of being in the treatment group.

The subject is not obese.

The subject is in the control group.

The subject has diabetes.

Now let’s estimate the propensity score for each subject. Because the left-hand side of the regression is a binary variable (whether the person is obese or not), we need to use a logistic regression. The propensity scores are the fitted (predicted) values from the regression. There are software packages that automatically estimate propensity scores and do the matching all in one line of code, but to understand the process of propensity-score matching, let’s write our own code to estimate the propensity score.

# Importing the toy data from a web link
obesity <- read.csv("https://bit.ly/obesity_toy_data")

# Model to estimate the propensity score
ps_model <- glm(obese ~ diabetes + age, data = obesity, family = "binomial")

# Saving the fitted values of the regression above as propensity scores
obesity$ps <- ps_model$fitted.values

import pandas as pd
 
# Importing the toy data from a web link
obesity = pd.read_csv("https://bit.ly/obesity_toy_data")
 
# Independent and dependent variables
feature_cols = ['diabetes','age']
X = obesity[feature_cols]
y = obesity.obese
 
# If you don’t have it installed, you can do so through pip by running ‘pip install -U scikit learn’
# You can check out full installation guide here https://scikit-learn.org/stable/install.html
 
from sklearn.linear_model import LogisticRegression
 
# Model to estimate the propensity score
ps_model = LogisticRegression()
 
ps_model.fit(X, y)
 
# Saving the fitted values of the regression above as propensity scores
obesity['ps'] = ps_model.predict(X)

* Importing the toy data from a web link
import delimited https://bit.ly/obesity_toy_data

* Model to estimate the propensity score
logit obese diabetes age

* Saving the fitted values of the regression above as propensity scores
predict ps

The following table shows the estimated propensity scores for each subject:

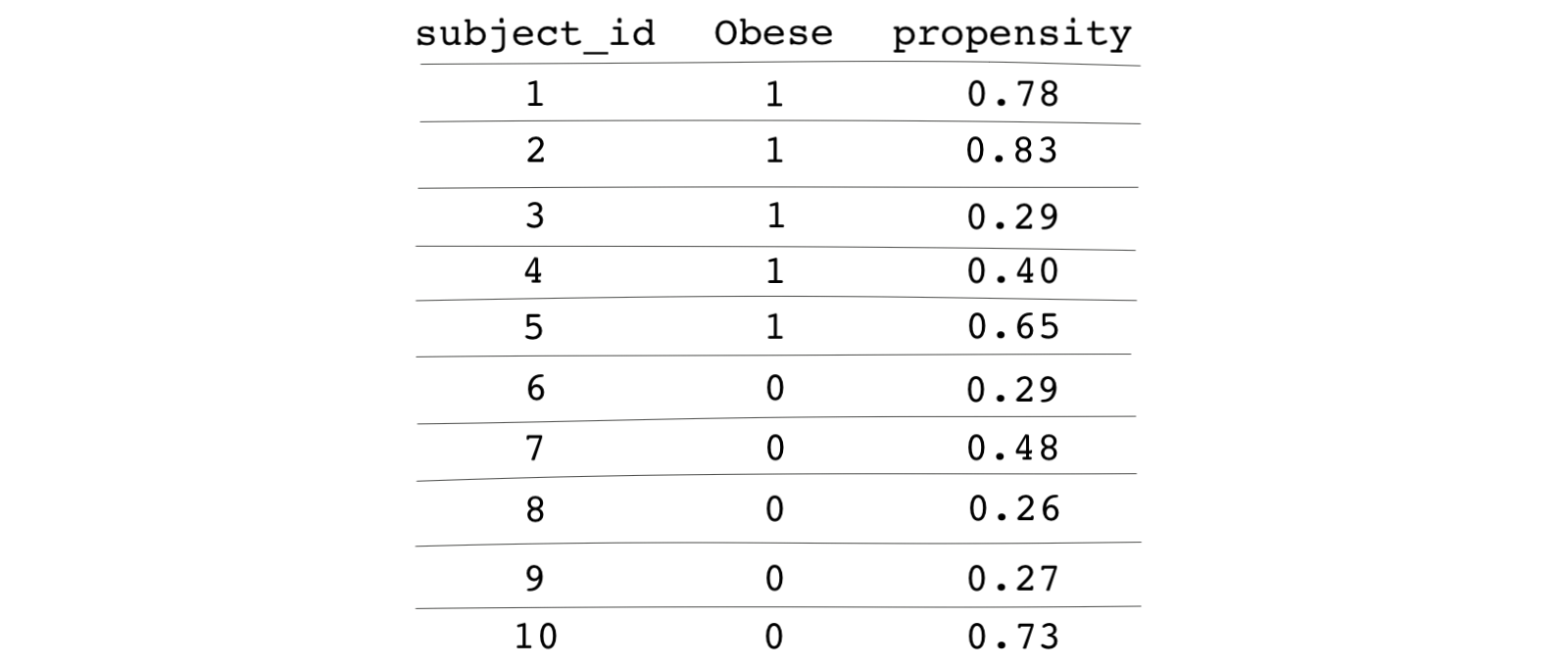
We can now start the matching process using these propensity scores!

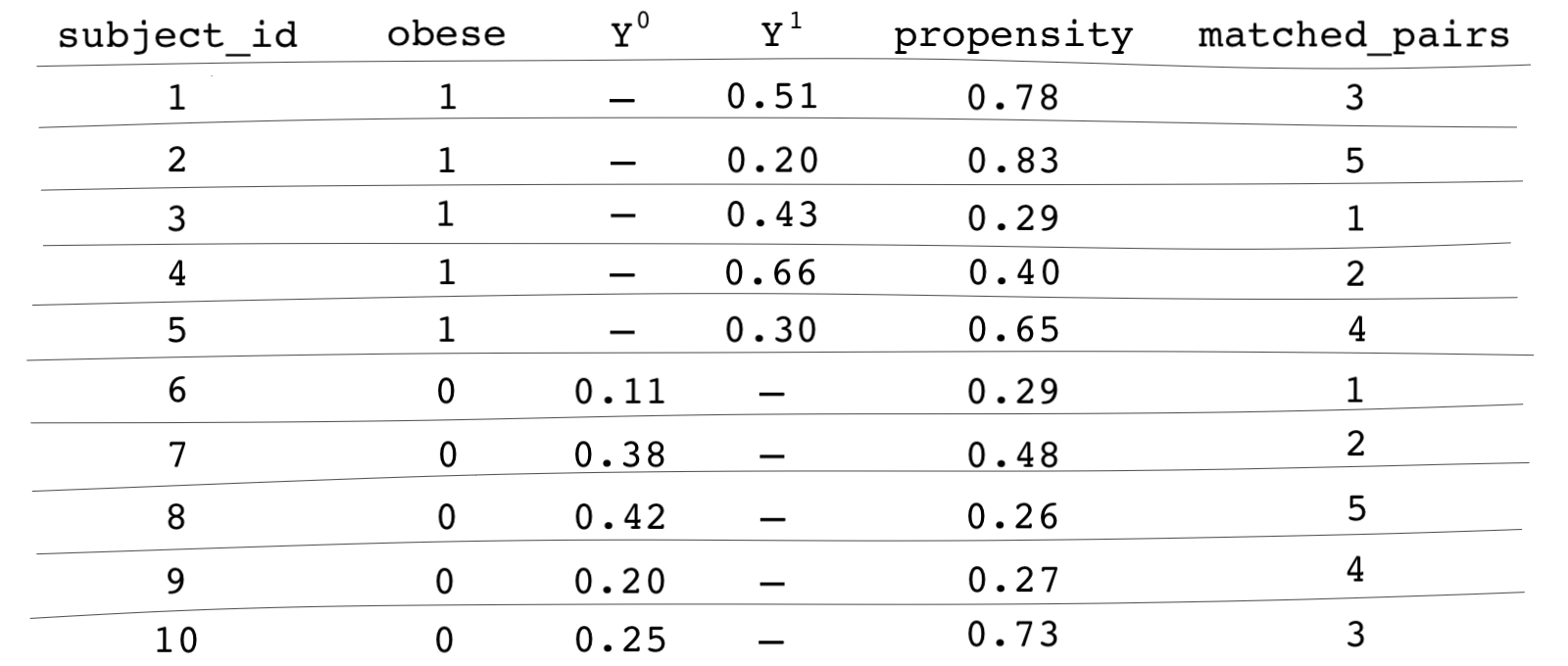
Let’s say we use greedy matching. We first pick a random treatment subject and find the closest control subject to it. Those matched observations will be put aside and we continue with the next random treatment subject. Let’s say the order in which we match treatment subjects is this: 3, 4, 1, 5, 2.

Starting with Subject 3, we find the subject has a propensity score of 0.29. Which control subject has the closest propensity score to 0.29? You guessed it, it’s Subject 6, which happens to have the exact same propensity score. Because we aren’t matching with replacement, and now that Subject 6 has been matched to Subject 3, remember that Subject 6 is no longer eligible for being matched with any other treatment unit. We now move on to Subject 4. In practice, we choose a caliper and call two observations matched if the distance between their propensity score is less than the determined caliper.

Imagine Subject 4 has a propensity score of 0.4. Which subject in the control group should we match it to?

You get the idea. We repeat this process until every treatment subject has a match or is dropped from the sample for lack of a match. Remember, greedy matching isn’t ideal especially when the dataset is small, but it’s easier to get familiar with matching methods using greedy matching, so that’s what we’ll use for now. The last column in our table indicates an id for each matched pair.

What now?

We’re almost done. The rest of the analysis is similar for any matching method we use ( Mahalanobis distance matching, propensity score matching, etc).

We can now easily estimate causal effects. We begin by filling in the unobserved potential outcomes of the treated units with their control counterparts’ potential outcomes. For instance, $Y_0$ for Subject 1 is unobserved, but we will assume it’s equal to its matched pair’s potential outcome, which is subject 10 with $Y_0$ equal to 0.25.

The table below shows all of the $Y_0$ cells filled in for the treated units. We don’t have to fill in the $Y_1$ cells for the control units because we want to estimate the average treatment effect among the treated (ATT) and not the ATE.

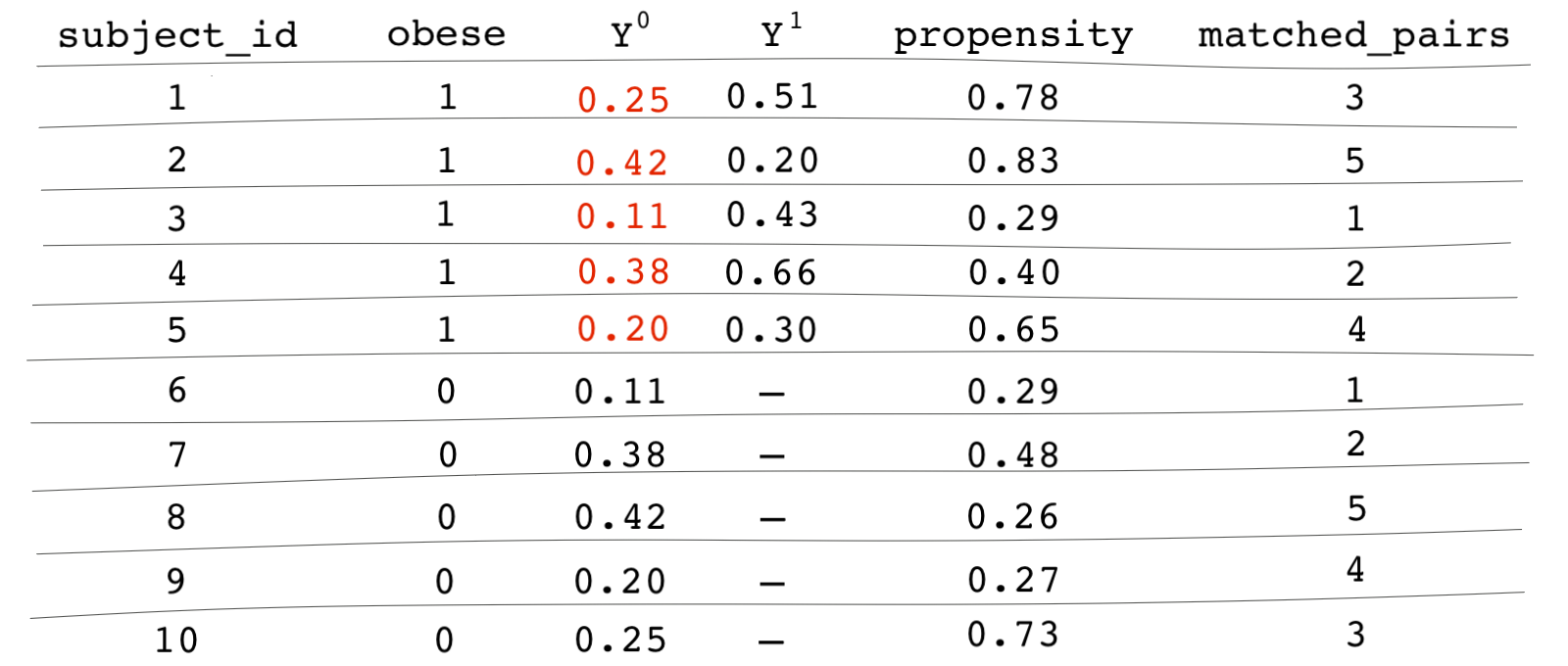
It seems like we somehow overcame the fundamental problem of causal inference. The missing values for the counterfactual outcomes of the treated units are replaced with the potential outcomes of their matched counterparts. We now have values for the potential outcomes of treated units under BOTH worlds: the world under treatment and the world under no treatment. To find the causal effect, we simply take the average difference between the two potential outcomes:

\text{ATT } = \dfrac{(0.51-0.25) + (0.20-0.42) + (0.43-0.11) + (0.66-0.38) + (0.3-0.2)}{5}

And just like that we have the ATT.

Next Lesson

Post-matching analysis

You'll learn about the basics of causal inference and why it matters in this course.