Covariate distance matching

In this lesson, we’re going to explore a question that came up in the previous lesson. When exact matches don’t exist, or are few and far between, what criteria should we use for matching and how do we assess the closeness (or distance) between subjects in the treatment versus control group?

Exact vs. distance matching

Exact matching is straightforward. We saw some examples of it in the last lesson. If you have a 34-year-old white male with no college education in the treatment group, you look for a 34-year-old white male with no college education in the control group. If you can’t find anybody, you drop the original observation in the treatment group.

This method is simple but not practical. The main issue is that when you have many covariates to match, finding exact matches becomes nearly impossible. If you can’t find an exact match and end up dropping many treated units, you’ll end up with a very small sample or no sample at all. On top of this, we’ll soon see that dropping treated units actually changes the interpretation of the causal effect.

Instead of exact matching, researchers tend to mix exact matching with covariate distance matching, or they might rely on covariate distance matching exclusively. In covariate distance matching methods, we allow for some distance between the observation in the treatment group and the observation in the control group (i.e., the observations don’t have to be exactly the same to be considered a match). To do this, we first define a caliper. A caliper is the maximum distance you want to allow between two observations. If the distance between observations is higher than the caliper, then we have not found a match, and we must continue to look for observations in the control group that are a match. If there are no matches for the treated observation whatsoever, then we drop that observation.

There are various ways to do covariate distance matching but the most popular one is Mahalanobis distance matching. Let’s take a 👀

Mahalanobis distance matching

Here we’ll return to the example in the previous lesson.

Imagine $X_i$ is the vector of covariates for subject $i$. For instance, if subject 1 has 16 years of schooling and is 47 years old, $X_1 = (16, 47)$ and if subject 2 has 17 years of schooling and is 31 years old, $X_2 = (17, 31)$.

Mahalanobis distance is a measure of distance between observations (or subjects) based on their covariates measured as follows:

where $S^{-1}$ is the inverse of the covariance matrix between the variables and is estimated as:

Here we’re assuming that the relevant covariates that block all backdoor paths have already been identified. But remember, finding covariates that satisfy the ignorability assumption is necessary before any matching methods can be applied. Once we have those covariates and know they’re available in the data, we match them. In this case, we are assuming the relevant covariates are years of schooling and age.

The algorithm for finding matches based on the Mahalanobis distance method is as follows:

1. Determine a caliper such as 0.25 (in practice and as a rule of thumb, we use 0.25 of the standard deviation of the logit of the propensity score)
2. Pick (usually at random) the first treatment unit.
3. Calculate the Mahalanobis distance of the observation with every single control observation
4. Pick the control observation that has the smallest Mahalanobis distance with the treatment observation in step 2. The distance should also be smaller than the caliper we determined in step 1. If there’s no match for the treated subject, drop (prune ✂) it.
5. Leave the already matched control and treatment observations aside and go back to step 2. Note that this method ignores a second treatment unit that better matches the already picked control unit. As we’ll see below, this method is called greedy matching.
6. Repeat until all treatment units have a match or are dropped because no match has been found.
7. Drop (prune) all the unmatched control units.

We mentioned that we only try to find one control match for each treated observation. This is called making a 1-to-1 match. This does not have to be the case.

Sometimes, we try to find more than one match for each treated subject. This is called k-to-1 matching with $k>1$. For instance, we commit to finding 3 control matches for each treated unit. We usually use 1-to-1 matching when the sample is small and use k-to-1 when the sample is larger. 1-to-1 may lead to lower bias of the causal estimates but with higher variances while the opposite is true for k-to-1. So we have a bias-variance tradeoff when it comes to choosing one over the other.

Sometimes we do a variable match, which means the number of observations in the control group that we match to each treated observation can vary and depend on how many good observations we can match. For example, for some treated subjects, we find 1, for others 2, for some others 3, and so on. You get the idea!

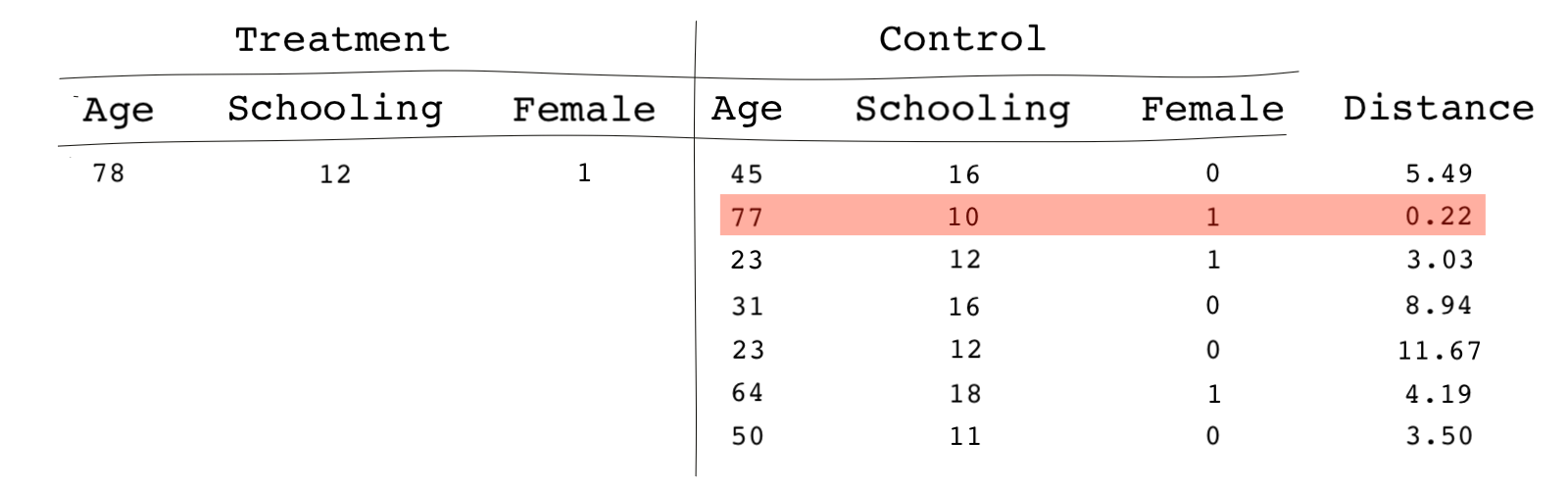
Note that we never use the main outcome variable in the matching process. In fact, this is one of the advantages of matching; the researcher does the matching process being blind to the outcome data and the causal estimates. The only objective during the matching phase is to achieve the best balance in the covariates.

Greedy vs. optimal matching

The method mentioned in the step 5 above is usually referred to as greedy matching.

It’s called greedy because the first treatment subject that’s drawn, has many more potential control subjects to be matched with. Once the control subjects are picked for those treatment subjects, they’re no longer considered for the following treatment subjects. In greedy matching, the initial treatment subjects usually have larger pools of control subjects to be matched with, but as matching takes place the pool of eligible control subjects dwindles, and the treatment subjects that happen to be last matched have a smaller chance of being matched or matched well.

The advantage of greedy matching is that it is fast. It’s fast because as we proceed, the pool of control subjects to consider as potential matches becomes smaller and smaller as we move on with the next treatment units. However, you can imagine that this method may not lead to the best results in covariate balance. The best control match for the first treatment subject may be an even better match for the second treatment subject, but that control subject is no longer considered for the second treatment subject.

This is why, sometimes, you should prefer to use optimal matching instead, especially when you have smaller data to match. In optimal matching, we find the distance of each treatment observation to every single control observation. You can see why this method takes longer and isn’t very efficient. For instance, if we have 1,000 treatment observations and 5,000 control observations, we need to find distance among 5,000,000 pairs (1,000 x 5,000).

Once we have all the distances, we choose matches holistically, meaning we keep an eye on a global distance measure and minimize that instead of individual distance measures. This global distance measure is usually calculated as the total distance between all the matches found.

This way we reduce the distance across all matched pairs rather than giving preferential treatment to the treatments that happen to be at the top of our list .

Some notes

It’s good to keep the following in mind when using matching methods:

• We mentioned briefly that you can mix exact matching with distance matching. This is typically done when some of your covariates are more important than others, especially if the important covariates are categorical variables (they include categories such as young, old, male, female, high school graduate, etc.). For instance, we might want to match male subjects with other male subjects and female subjects with other female subjects. So we want to do exact matching on the variable gender. If this the case, you can allow your algorithm to do exact matching on certain covariates and distance matching on others.
• Exact matching methods don’t work well when there are many covariates to match on. When there are many dimensions to match on, using exact matching may lead to many unmatched observations. When this is the case, we can use a variant of exact matching called coarsened exact matching. We categorize (bin) continuous variables into groups then match on these new variables. For instance, instead of using age as a continuous variable, we can categorize a variable representing age by grouping subjects into those who are 20-40 years old, those who are 40-60 years old, etc.
• If there are outlier values for certain covariates, Mahalanobis distance matching may lead to large distances between subjects even if subjects are close in terms of other covariates (those without outliers). To prevent this, we use a method called robust Mahalanobis distance matching, which uses a ranking in place of distance. If parental income is one of the covariates and has outlier values, we can replace each value across the treatment and the control observation with a rank. The lowest parental income gets a rank of 1, and the second-lowest gets a rank of 2, and so on. We then match based on rank values instead of the actual income values. For instance, an observation with the highest parental income in the treatment group is matched to an observation with the highest parental income in the control group even if the first value is 500,000 dollars and the second value is 300,000 dollars.
• One other variation to the matching methods we’ve seen is matching with replacement. In matching with replacement, we can reuse an already matched control subject for another treatment subject. This method may reduce bias in the causal estimates. This method is especially useful when the share of control observations to treated observations is small. The nice thing about matching with replacement is that the order in which we match treated subjects no longer matters. However, in matching with replacement, we change the structure of the sample in the sense that the control group we end up having is no longe the original control group we started from (three are repeated control subjects in it)
• When the covariates have non-normal distributions, the Mahalanobis distance matching doesn’t perform well. Another method that has become popular is called genetic matching. Genetic matching is based on a search algorithm that iteratively checks and improves covariate balance. Genetic matching, in essence, is very similar to Mahalanobis distance matching. The algorithm’s objective is to minimize the overall imbalance of the covariates across the treatment and the control groups based on p-values from a test called the Kolmogorov–Smirnov test or simply the KS-test (among other tests) for all variables that are being matched on. These tests quantify the closeness of two covariate probability distributions.