Working through an example

You have learned enough to go through an empirical study using matching on your own. In this example, we’ll see how you use matching, assess your matching results, and then use those results to estimate causal effects. Let’s get to it! 💪🏼💪🏼💪🏼

Do populist policies increase an incumbent party’s votes?

Do populist policies implemented to boost political support for the incumbent party result in success in future elections. Data that can help us answer this question is limited, but luckily we have data to do a causal study in Brazil 🇧🇷. This was a question raised and answered by Cesar Zucco in his 2013 paper.

Voting behavior may be affected by programs that are economically beneficial to voters in the short-term. Zucco is more interested in cash transfers. He uses observational data from Brazil’s Conditional Cash Transfer (CCT) programs in the cities of Campinas and Brasilia. These two cities began making cash payments to low-income families upon the condition that they keep their children in school and regularly visit a doctor. To answer whether such policies affected voter’s behavior isn’t an easy causal question to answer. For starters, how would you make the case that it was the cash transfer program, specifically, which made an impact on voters and not any of the other policies implemented by the incumbent?

Similar to an example we saw earlier in this module, it will be a challenge to differentiate between general support for the incumbent prior to treatment with support for the incumbent during the following election. Furthermore, there are likely differences in the pre-treatment distribution of covariates (the main covariate being the political leanings of those in the treatment and control groups).

To tackle this causal question, Zucco starts by using propensity score matching. Here we are going to show a simplified version of the matching method used in the paper. More information about the data can be found here. For your convenience, you can download the data directly to your software using the following commands:

# Importing the data from a web link
# Original dataset can be found here:
# https://dataverse.harvard.edu/dataset.xhtml?persistentId=hdl:1902.1/20257
cash_voting <- read.csv("https://bit.ly/cash_voting")
# Because some matching algorithms don't like missing values, 
# we've already gotten rid of missing values first.
# But we don't want to get rid of the missing values in all variables.

# Importing the data from a weblink
# Original dataset can be found here:
# https://dataverse.harvard.edu/dataset.xhtml?persistentId=hdl:1902.1/20257

import pandas as pd
df = pd.read_csv("https://bit.ly/cash_voting")

# Because some matching algorithms don't like missing values, 
# we've already gotten rid of missing values first.
# But we don't want to get rid of the missing values in all variables.

* Importing the data from a web link
* Original dataset can be found here:
* https://dataverse.harvard.edu/dataset.xhtml?persistentId=hdl:1902.1/20257
import delimited https://bit.ly/cash_voting

The main variables we’re going to use from the data include:

voted: Whether the individual voted for the incumbent party’s (Worker’s Party) candidate. The candidate was Dilma Rousseff.
beneficiary: Whether the individual was a beneficiary of the cash transfer program
female: Whether the individual is female
age
yrs_school: Years of schooling of the individual
nonwhite: Whether the individual is not white
metropolitan: Metropolitan municipality of the individual
hdi_2000: Human Development Index (HDI) of the municipality in 2000
growth: Growth rate of the region individual resides in over the previous year
distcap: Distance to capital city (in km/10)

The variables voted and beneficiary are both binary variables.

In the data, how many of the observations are in the treatment group?

Too lazy to calculate that

831

572

356

Now, let’s do some matching. We’ve identified that variables female, age, yrs_school, nonwhite, metropolitan, hdi_2000, growth, and distcap satisfy the ignorability assumption, i.e., controlling for them prevents any confounding in the estimates.

For matching, we will:

use a simple nearest-neighbor propensity score method
match with replacement
use a ratio of two-to-one for each treatment. In other words, we’ll do our best to match two control subjects to each treatment subject.

All of this can be done using readily available matching functions that come with most statistical software:

# If you don't have the package MatchIt installed, first install it
# install.packages("MatchIt")
# note: You can alternatively use the package Matching
# load the library for matching analysis
library(MatchIt)

# Doing the nearest-neighbor matching based on propensity scores.
# The method we use below is to find pairs of observations that have
# very similar propensity scores, but that differ in their treatment
#  status. We use the package MatchIt for this.
# This package estimates the propensity score in the background 
# and then matches observations based on the method of choice (“nearest” in this case).
# change method to "optimal" for optimal matching, "exact" for exact matching,"
# full" for full matching, "genetic" for genetic matching, "subclass" for subclassification,
# also replace = FALSE indicates matching with no replacement. Ratio indicates the number of control
# subjects matched to each treated subject. Change these parameters to see how your results
# change.
matched_output <- matchit(beneficiary ~ female + age + yrs_school + nonwhite + growth +
                          hdi_2000 + I(hdi_2000^2) + distcap + metropolitan, data=cash_voting,
                          method = "nearest", replace = FALSE, ratio = 1) 

# Check the summary of matching including the standardized bias in 
# both treatment and control groups before/after matching
summary(matched_output)

# Python codes will be added soon

* If you don't have the package MatchIt installed, first install it
* ssc install psmatch2, replace

* Doing the nearest-neighbor matching
* You can change the method to other methods.
* Read here to learn more: http://repec.org/bocode/p/psmatch2.html
* n(1) sets the number of neighbors used to calculate the matched outcome. In other words,
* it indicates the number of control subjects matched to each treated subject.
* Change these parameters to see how your results change.
* noreplacement indicates matching with no replacement.
psmatch2 beneficiary female age yrs_school nonwhite growth ///
hdi_2000 c.hdi_2000#c.hdi_2000 distcap metropolitan, n(1) outcome(voted) noreplacement

* Check the summary of matching including the standardized bias in 
* both treatment and control groups before/after matching
pstest female age yrs_school nonwhite growth ///
hdi_2000 distcap metropolitan, both

Note that the left-hand side of the regression in the function is the treatment variable: beneficiary. We can see that we have 696 control subjects and 356 treated subjects after dropping observations with missing values. When we do matching, only 318 subjects in the control group are matched, and the remaining 378 aren’t matched. Every observation in the treated group is matched.

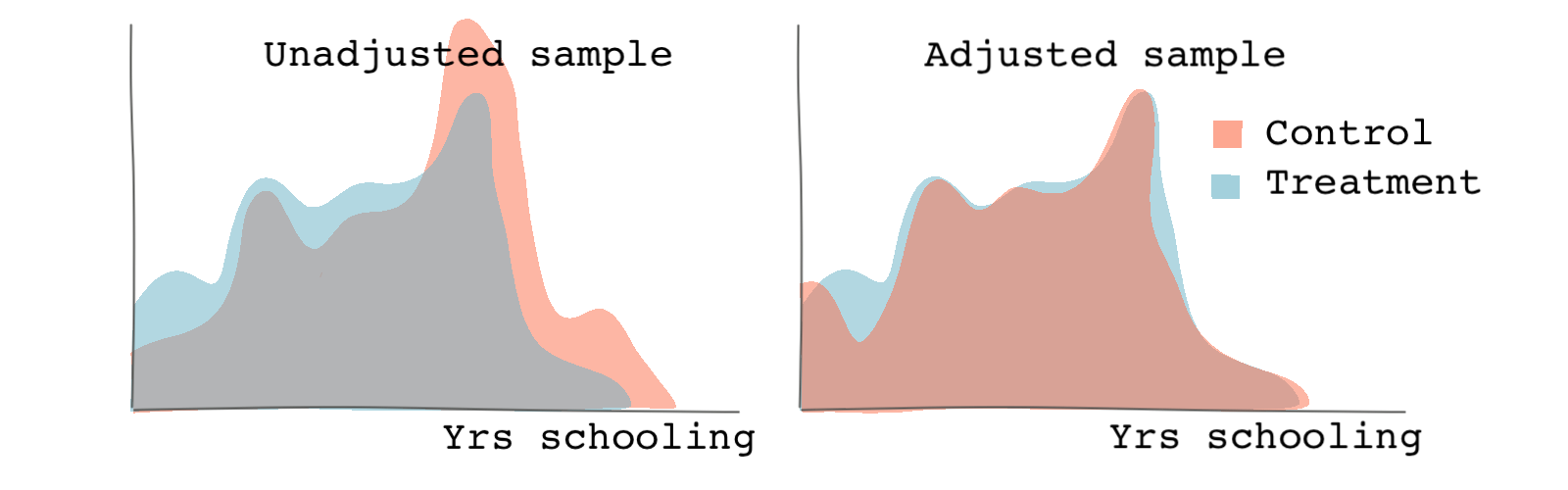
Let’s look at covariate balance for both the propensity scores and the variable yrs_school before and after matching.

# cobalt is a package that provides balance assessment tools
# in a more visually pleasant way. It shows balances before and after matching.
# It can be used in conjunction with the package MatchIt. The output of matchit
# function can be used as an argument in functions from the cobalt package.

library(cobalt)
# We can specify the name of the covariate we're checking for balance. 
# the function bar.plot shows the histogram or density functions of the 
# variable specified. If we specify which as both, we will see both the
# unadjusted (original) and adjusted (matched) samples.
# The following checks plots the density plots of the propensity scores.
bal.plot(matched_output, var.name = "distance", which = "both")

# The following checks plots the density plots of the variable years of
# schooling
bal.plot(matched_output, var.name = "yrs_school", which = "both")

# Python codes will be added soon

* Distribution of propensity scores before matching
twoway (kdensity _pscore if _treated==1) (kdensity _pscore if _treated==0, ///
lpattern(dash)), legend( label( 1 "treated") label( 2 "control" ) ) ///
xtitle("Propensity scores before matching") name(before, replace)

* Distribution of propensity scores after matching
twoway (kdensity _pscore if _treated==1 [aweight=_weight]) ///
(kdensity _pscore if _treated==0 [aweight=_weight] ///
, lpattern(dash)), legend( label( 1 "treated") label( 2 "control" )) ///
xtitle("Propensity scores after matching") name(after, replace)

* Both graphs combined
graph combine before after

* Distribution of variable yrs_school before matching
twoway (kdensity yrs_school if _treated==1) (kdensity yrs_school if _treated==0, ///
lpattern(dash)), legend( label( 1 "treated") label( 2 "control" ) ) ///
xtitle("Years of schooling before matching") name(yrs_before, replace)

* Distribution of variable yrs_school after matching
twoway (kdensity yrs_school if _treated==1 [aweight=_weight]) ///
(kdensity yrs_school if _treated==0 [aweight=_weight] ///
, lpattern(dash)), legend( label( 1 "treated") label( 2 "control" )) ///
xtitle("Years of schooling after matching") name(yrs_after, replace)

* Both graphs combined
graph combine yrs_before yrs_after

We can see from the graph below that matching leads to more similar probability distributions between the treatment and control groups compared to the unadjusted (unmatched) sample.

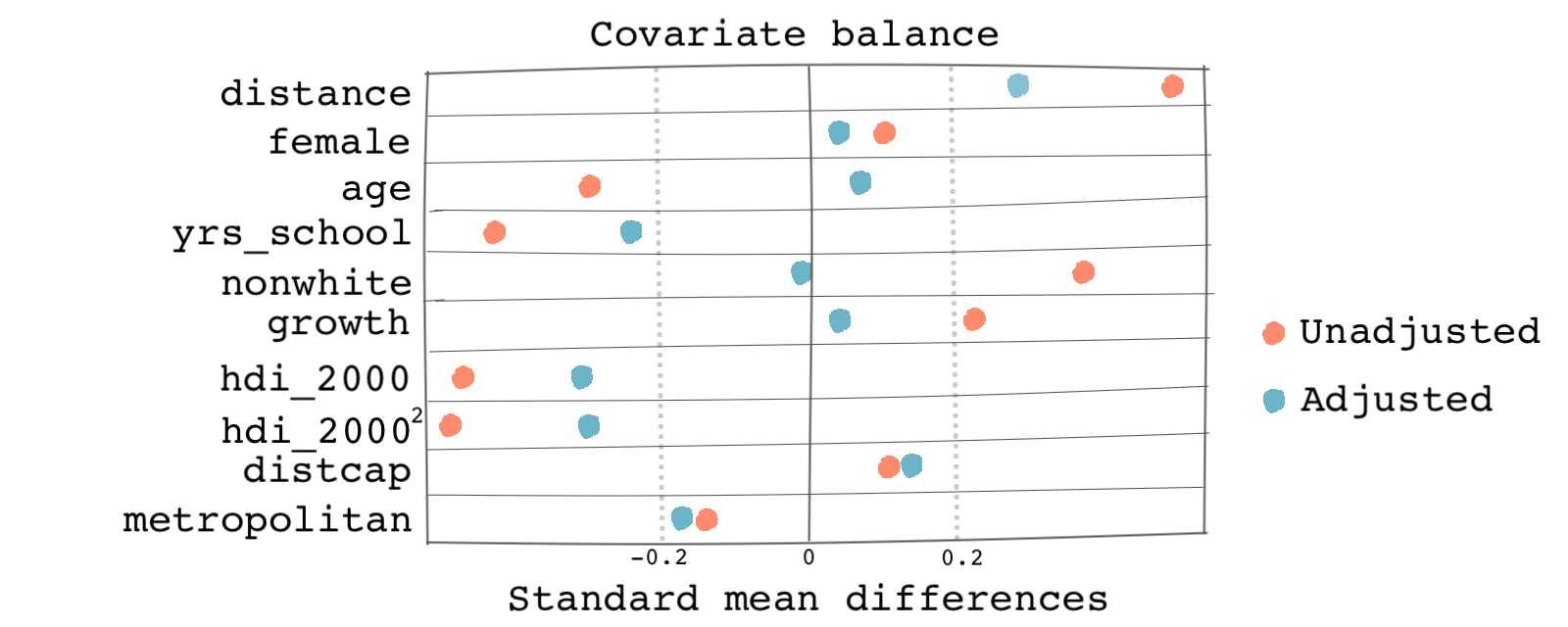
There is also a cool visual way of checking covariate balance. This method employs a plot called the Love plot, a summary plot of covariate balance based on the standardized biases. The plot shows the standardized mean difference between observations in the treatment and the control groups before and after matching. Here’s how:

# In R, We can specify the threshold as 0.2 which can be seen as the 
# upper limit for a good match
love.plot(matched_output, binary = "std", thresholds = c(m = .2))

# Python codes will be added soon

* In Stata, the standardized biases are in percentages.
pstest female age yrs_school nonwhite growth ///
hdi_2000 distcap metropolitan, both graph

Based on the graph below, we can see that covariates in the matched (adjusted) sample are more balanced than the same covariates in the unadjusted sample. The absolute values of the standardized mean differences are within the range 0.2.

You can change your matching parameters or even the method to make the results even better. Given that we’ve done a good job with matching, let’s get to the last step. We’re going to estimate the causal effect of receiving cash transfers on voting for the incumbent party. This part is easy. We can just use linear regression controlling for the same covariates we matched on. However, be careful to use the matched dataset and not the original dataset.

# We need to first create a dataset of the matched data
# The argument distance = "pscore" include a variable in the new dataframe
# that is the propensity scores.
matched_data <- match.data(matched_output, distance ="pscore")

# Analaysis with the matched dataset
# We use the glm function and family = binomial() because the dependent variable is
# binary and we want to do a logistic regression.
fit_matched <- glm(voted ~ beneficiary + pscore + female + age + yrs_school + nonwhite + growth +
                           hdi_2000 + I(hdi_2000^2) + distcap + metropolitan, 
                   family = binomial(), data = matched_data)

# summary of the regression results
summary(fit_matched)

# Python codes will be added soon

* Package psmatch2 makes it easy by creating a _weight variable automatically.
* _weight is 1 for observations in the treatment group and for observations in the control
* group it is the number of observations from the treated group for which 
* the observation is a match. If the observation is not a match, _weight is missing.
* We can easily estimate the treatment effect by using the logit function (because
* the dependent variable, voted, is binary.
logit voted beneficiary pscore female age yrs_school nonwhite growth ///
hdi_2000 c.hdi_2000#c.hdi_2000 distcap metropolitan [fweight=_weight]

The coefficient on our treatment variable beneficiary is 0.54. We interpret the coefficient as if the percent is a beneficiary of the cash-transfer program, the log odds ratio of voting to the incumbent candidate increases by 0.54.

How different would the result be if we used the original data without doing any matching? Well, we can easily check that:

# Analaysis with the original dataset
fit_unmatched <- glm(voted ~ beneficiary + female + age + yrs_school + nonwhite + growth +
                             hdi_2000 + I(hdi_2000^2) + distcap + metropolitan, 
                     family = binomial(), data = cash_voting)

# summary of the regression results
summary(fit_unmatched)

# Python codes will be added soon

* Analysis with the original dataset
logit voted beneficiary female age yrs_school nonwhite growth ///
hdi_2000 c.hdi_2000#c.hdi_2000 distcap metropolitan

For the unmatched data, the causal effect is 0.41 which is very different than the one from the adjusted sample.

Next Lesson

Pros and cons of matching

You'll learn about the basics of causal inference and why it matters in this course.

Go to the next lesson

All Courses

Working through an example

Do populist policies increase an incumbent party’s votes?

Next Lesson

Pros and cons of matching