Post-matching analysis

Because there are many approaches to matching, researchers use a trial-and-error approach to figure out which method to use. If a given method produces unsatisfactory covariate balances, you can always try a different method or tweak the parameters of the method you’ve used. You can do this by:

• changing the caliper,
• choosing k in k-to-1 matching or choosing variable matching,
• switching between matching with our without replacement
• or using exact matching for certain covariates and nearest-neighbor matching for others.

We can also use a method called sub-classification in which, instead of finding matches for each treated subject, we find a match for a cluster of treated subjects. This can be done by defining $m$ clusters (usually 5-10). In the end, we estimate causal effects based on the potential outcomes of the clusters rather than the potential outcomes of the treated subjects.

A similar method to sub-classification is called full matching, in which the algorithm automatically finds the number of clusters and all of the control units get matched to one of the clusters. In full matching, each group should contain at least one treated and one control subject.

Other modifications we can do to achieve a better balance of the covariates is to include in the propensity score regression model interaction, quadratic, or cubic terms and variables beyond the initial set. In her 2010 paper on matching methods, Elizabeth Stuart suggests including variables that are actually not associated with the treatment variable in matching as there will be little cost in including them. However, she warns that including variables that are not associated with the outcome in the matching process may lead to slight increases in the variance of the causal estimates. In any case, excluding potentially relevant variables can be a lot more costly and so it’s ok to be a little relaxed when it comes to including variables.

It’s perfectly ok to do the matching analysis using parameters and methods and see which leads to a better covariate balance as long as we don’t look at the causal effect. It’s also ok to include variables beyond the ones that cause confounding bias.

However, the important point is that we should not adjust the parameters, methods, or variables based on the causal effects we find. We should be blindfolded about the causal effects as we do the matching analysis. Looking at the causal effect estimate may trigger some bias in choosing one matching analysis over another. But achieving covariate balance as an objective is good practice.

Checking for covariate balance

We have stated multiple times that the goal of matching is to achieve covariate balance, but how do we determine whether the balance we achieved is good enough? Balance is defined as the similarity of each covariate distributions in the matched treated and control groups.

A straightforward way to check covariate balance is to look at the standardized bias. Standardized bias is the difference in the means of a covariate between the treatment and controlled observations divided by the pooled standard deviation (all observations) as follows:

We should compute the standardized bias before matching and check how the measure changes after matching. Ideally, we want the standardized bias to shrink for each covariate. As a rule of thumb, a standardized bias smaller than 0.1 is considered good and a standardized bias smaller than 0.2 is acceptable.

We can then show the standardized biases in one plot for before (unadjusted) and after matching (adjusted) like the one shown below. In this figure, you see that matching actually reduces the standardized bias in almost all covariates.

Practice

Look at the chart above. For which of the covariates is the standardized bias actually higher after matching?

Female

Share married

Years of schooling

Number of children

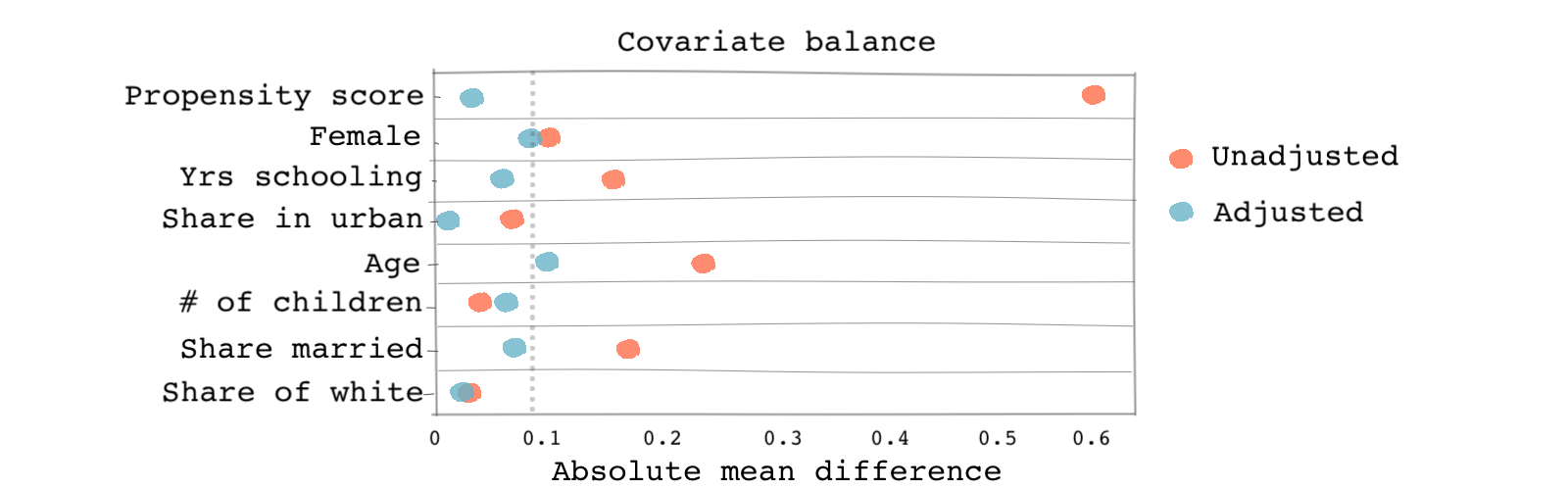
Although standardized bias is relatively easy to check, it will not always give you all of the information you need to assess the full distributional differences pre and post matching. Remember, the standardized bias is only comparing the mean of the distribution; it isn’t comparing the full distribution. For this reason, it helps to look at a histogram of the covariates. If matching does a good job, the distributions become more similar after matching. The figure below shows how the distribution of the age covariate becomes more balanced after a hypothetical matching exercise.

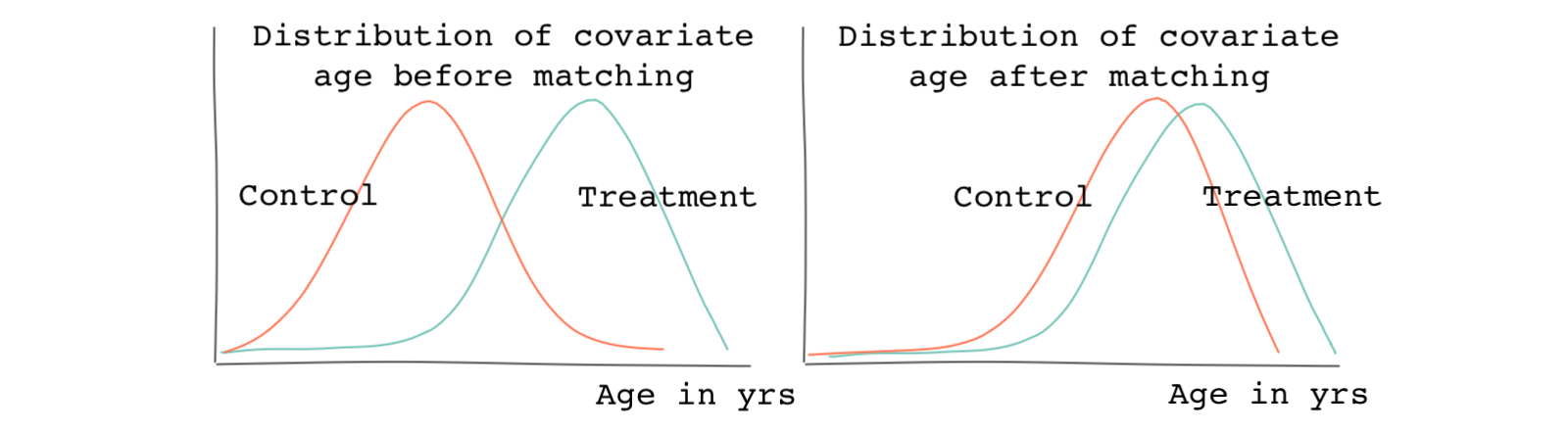
We should do a similar comparison for each covariate. As an alternative to looking at histograms, there are statistical tests for measuring the similarity between two probability distributions. Researchers use a test called Kolmogorov–Smirnov test or simply the KS-test to measure the closeness of two distributions.

But if we have many covariates to match on, it becomes a tough task to make sure matching leads to better covariate balance across all of the covariates, especially if we’re comparing various matching approaches and want to know which one leads to better balance. What do we do in these situations?

In such situations, we can look at the worst covariate balances after matching. We then choose a matching method that leads to the best worst balances, i.e., when the worst covariates in terms of the balance are better when compared to other matching methods.

Checking for balance when using propensity-score matching

Remember that propensity-score matching works a bit differently than all of the other matching methods we’ve covered. Because the propensity-score represents balance across all covariates, we do not need to check for balance covariate by covariate when using this method. We simply need to compare the propensity scores pre- and post- matching to check for balance.

As we saw before, a quick test would be to check whether the distribution of the propensity scores for the treated group versus the control group overlaps after matching. Matching is considered poor if there’s not much overlap. If we can’t improve the overlap by trying various methods, we can only estimate the causal effect for observations in the overlapping region.

In propensity-score matching, Rubin suggests two additional metrics for assessment:

• The standardized bias for the propensity score (similar to the one we defined for covariate-distance matching)
• The ratio of the variances of the propensity score in the treated group to that of the control group

Having said this, we’ll see in an upcoming lesson that a better practice in propensity-score matching is to check for balance in all covariates and not just the propensity score. Propensity score matching sometimes leads to certain covariates being less balanced than before and those covariates might be important for us.

Using regression together with matching

As we saw in the short example at the end of the previous lesson, matching allows us to estimate the unobserved potential outcomes for each treated unit in our sample that has a match. This allows us to compare the potential outcomes under treatment to potential outcomes under no treatment and estimate a causal effect. And this is why matching, under certain assumptions and if done correctly, helps us overcome the fundamental problem of causal inference.

Straightforward and simple as this line of reasoning may be, matching alone is insufficient for coming up with a good estimate of causal effects. Even if you analyze your match results and strive to use the best matching methods available, discrepancies between the distribution of covariates in your control and covariates in your treatment can remain. Similar to how we use regression analysis to fine-tune randomized experiments, we can use regression and matching to improve causal estimates in observational studies. We’ll see an empirical example of how to do this in the next lesson.

So we simply pool all the matched observations and use the covariates we use to match on as our control variables. We also include the treatment variable. The variable on the left-hand side of the regression will be our outcome variable.

If we used propensity-score matching, it’s better to include the vector representing the propensity scores among the covariates on the regression’s right-hand side to further correct for imbalances. We will see an empirical example in the next lesson.

ATT versus ATE

Before moving on, there’s one final catch to matching. In most matching methods, we only estimate the average treatment effect among the treated (ATT) and not the population average treatment effect (ATE). This is not too bad because, as we saw before, in most disciplines, we’re mostly concerned with ATT and not ATE.

But why is it the case that matching leads to estimating ATT? This can be explained by how we usually match: we usually start with the treatment group and look for matches in the control group. In most cases, the final matched sample contains most of the treatment observations and only a subsample of the control observations. In fact, the more control subjects we drop (prune), the closer the estimated causal effect gets to ATT and the farther it gets from ATE.

Although we will not deal with them directly in this course, you should know that there are also matching methods designed specifically for estimating ATE rather than ATT.

In the case where we are mostly concerned with ATT, we do not have to worry about the ATE, but we should be concerned about the unmatched treated subjects. For instance, we saw if the distributions of the propensity scores for treated and control subjects don’t overlap much, we can only estimate the causal effect for the observations that lie in the overlapping region. If many observations from both the treatment or control groups don’t fall in the overlap region, then the estimated causal effect is not representative of ATT or ATE.