The basics of matching

In the previous module, we used DAGs to identify variables that cause confounding bias. By controlling for these variables, we can satisfy the ignorability assumption, meaning we can reasonably estimate a causal effect without worrying about confounder bias.

Knowing this, we are ready to delve into different methods for estimating causal effects. In this module, you’ll be learning two methods: matching and inverse probability weighting.

What is matching?

To understand matching, we need to revisit the difference between randomized experiments and observational studies. Recall that the most important characteristic of a randomized experiment is that subjects are randomly assigned to treatment and control groups. Researchers usually use computer algorithms to do this, but they could just as well use a primitive method such as flipping a coin or drawing straws.

Imagine you’re conducting a randomized experiment with one control group and one treatment group. You assign subjects to the treatment or control using a flip of a coin (heads, treatment; tails, control). Suppose that you have 30 female subjects within your study. Because the flip of the coin lands on heads and tails with equal probability, and because the results of the flip are entirely random, you’ll likely end up with close to half of the females in the treatment group and roughly half in the control group. The same goes for other major characteristics within your sample, such as level of education, age, health measures, etc.

Now, let’s say your study’s goal is to estimate the causal effect of providing individuals with additional information about a specific government program. Your outcome variable is support for the program. In other words, you want to see if providing additional information about the program increases support for it. In the absence of randomization, age, gender, and education level are likely all confounders. The political affiliation of your subjects would be another confounder that could skew your results. Intuitively, it’s not hard to imagine why this is the case. If your treatment group was dominated by subjects with political leanings already sympathetic to the goals of the government program, and your control group was dominated by those who had opposing political views, your results could easily overestimate the effects of the treatment. Your result might show a high level of support for the program among the treatment group and a low level of support among the control group. Still, the results could have nothing to do with the treatment (exposure to additional information about the program) and everything to do with the imbalance in political leanings between them.

Through randomization, we help to ensure that such a scenario doesn’t occur. Randomization is used to achieve a balance between the treatment and control groups (subjects exhibiting characteristics that might otherwise bias your results are roughly equally distributed between treatment and control), and thus, you can be confident that differences in average outcomes between the control and treatment group are, in fact, due to the treatment. Without randomization, you’re comparing 🍎🍎 to 🍊🍊. With randomization, you’re comparing 🍎🍎 to 🍎🍎.

In observational studies, all of this is not so easy. Unlike randomized experiments, in observational studies, subjects typically “self-select” into treatment and control groups. This results in selection bias, which if ignored, will skew your results.

Going back to our example, let’s imagine that we are now using an observational study rather than a randomized experiment to estimate the causal effect. Rather than providing the additional information to a carefully selected treatment group, you will now ask participants how much information they have been exposed to about the specific government program. It’s not hard to imagine how selection bias could creep in here. Those already in favor of the program may have been more likely to seek out additional information about it, or they may have had more exposure to additional information via the social circles they run in or the type of news they follow. If this is the case, we’re back in the realm of comparing 🍎🍎 to 🍊🍊

Let’s consider another example.

Think about a study designed to estimate the causal effect of taking two medication types on future health outcomes. If participants self-select into the treatment by choosing the type of medication they take, we will likely run into selection bias problems.

Here is where everything we learned in the previous module about identifying confounders comes into play 👇

The basic idea of matching is to match subjects in the treatment group to those in the control group using the information you have about confounding variables. Imagine that in your observational study, 30 percent of the treatment group is >50 years old. Meanwhile, 45 percent of the control group is >50 years old. The goal of matching is to rebalance the treatment and control groups as if this characteristic was similarly distributed across the treatment and control. Matching readjusts the treatment and control groups to ensure that every subject in the treatment group has a similar counterpart in the control group and that every comparison drawn in your analysis is between matched subjects. We’ll see an example of how this is done in a minute, but the basic idea is this: through matching, we are trying to make our treatment and control group as close as possible to what would occur in a randomized experiment.

By matching on a set of covariates, we can achieve covariate balance, i.e., the distribution of each covariate will be similar across the treatment and the control groups. Once we achieve covariate balance, we can safely assume that comparing the treatment and the control group is an 🍎🍎 to 🍎🍎 comparison and that the difference in average outcomes across the treatment and control will be a good estimate of the causal effect.

A simple example with only one confounder

Let’s revisit the job training example where the treatment is job training and the relevant outcome variable is earnings!

Assume now that we are conducting an observational study, and therefore, the treatment is not randomly assigned. After constructing the DAG for this causal question, we find that the single most important confounder is prior educational attainment, and this variable needs to be controlled for. By controlling for education, all backdoor paths between the treatment and the outcome are blocked. Further, assume that the variable in our data that captures education is binary: it’s equal to 🔵 (blue) if the person has a college degree and 🔴 (red) otherwise.

The following table shows subjects in the treatment and the control group color-coded based on their educational attainment. Again, 🔵 for those who have a college degree and 🔴 for those who don’t.

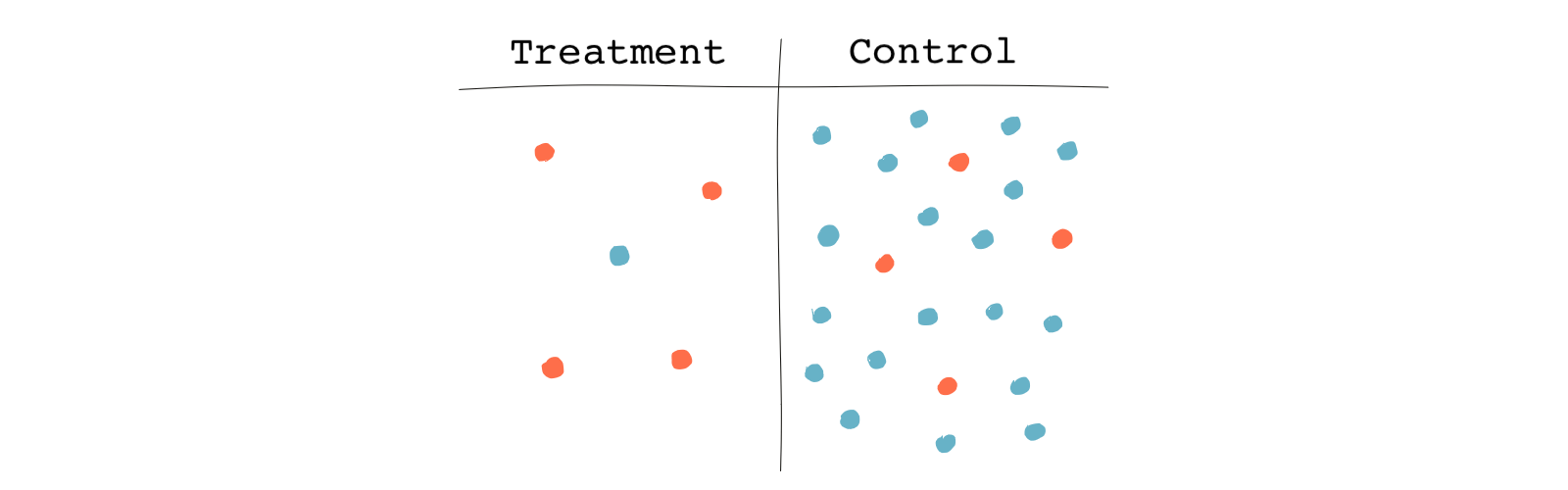
From the table, we see a higher share of non-college-educated subjects in the treatment group than in the control group. 80% of those in the treatment group are not college-educated compared to only 20% in the control group. So when it comes to our main confounding variable, the two groups are not very similar.

Since we’ve determined that education is a pretty good predictor of who gets treated, we need to control for it. This is where matching can help. By matching, we try to find a match for each treated unit. If there is a treatment unit without a match, we’ll discard it. If there are additional control units that don’t have a match, they’re discarded as well. Here, because there’s only one covariate, the task is very easy.

The following table shows the matched pairs.

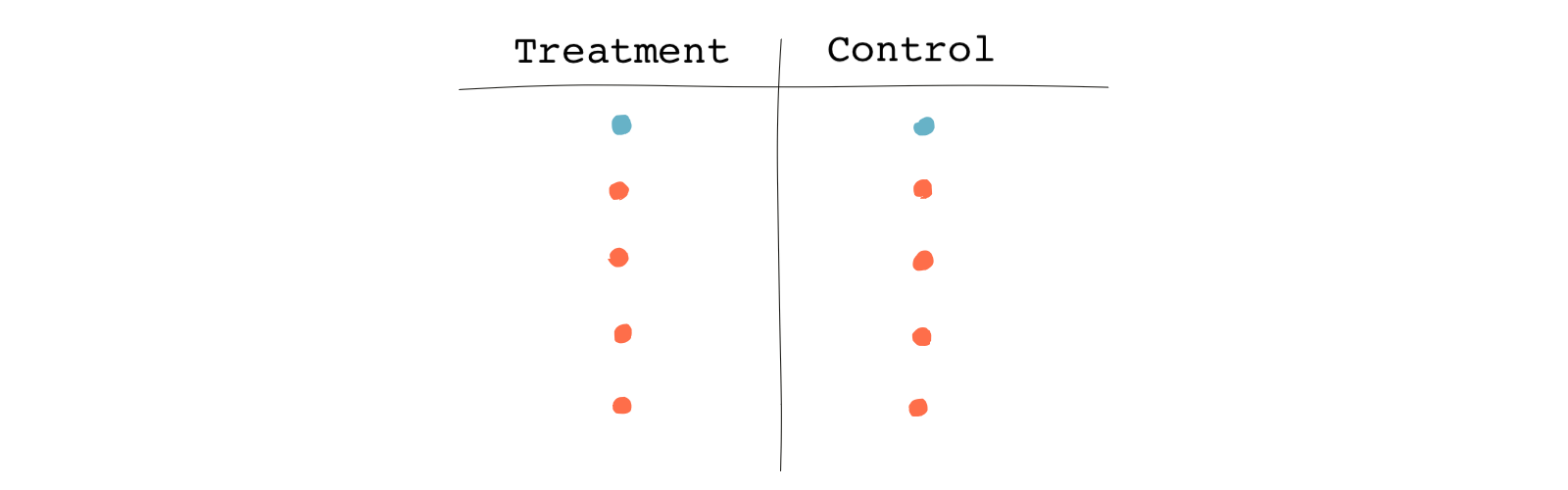
Based on this table, it’s obvious that we found a match for every treated subject, but some of the control subjects were unmatched, so they were discarded. This is why the resulting sample is smaller than the original one. In this case, we now have a perfect balance in terms of our single covariate, college education. Note that finding perfect matches and discarding unmatched subjects is only one approach to matching.

When we have more covariates, the task of matching isn’t as simple.

An example with more covariates

Now, consider that we were wrong about the DAG we just drew. We’ve re-examined our assumptions and have determined that we need to control for another covariate to block all backdoor paths (did you already forget what backdoor paths are? 🤦🏻‍♀️).

The additional variable we need to control for is age. Moreover, we realize a better measure of educational attainment is to use a continuous variable reflecting years of schooling instead of a binary variable just indicating whether a person is college-educated or not.

The following table shows subjects in the treatment and control groups. Each subject is represented by two numbers, the first number indicating their years of education and the second number indicating their age. (It might be clearer if you keep a circle around each observation.

By looking at the table, we can find an exact match for only one of the treated units (16, 47). For one of the other treated units, we can find a pretty close (but not exact) match. For the treated subject (10, 56), the closest match in the control group is (10, 57), which seems close enough to call a match. The two subjects have had the same years of schooling and only differ in age by one year. But where would you draw the line? In matching, the criteria for determining a match is up to the researcher’s discretion and should be based on clear and well thought out reasoning. Note that the unmatched units in the control group were discarded in this case.

Because of the simplicity of this example (we were only looking at two straightforward variables), we were able to find and designate pretty close matches. The more confounders you have to deal with and the more observations you have, the more involved the matching process becomes. And it’s not always easy to define closeness **(what’s close enough or closer when considering whether observations should be matched). Consider the following pairs:

• (10, 56) in the treated and (10, 57) in the control
• (10, 56) in the treated and (11, 56) in the control

Which one of the pairs are closer to each other?

In the next lesson, we will go over some methods for calculating the closeness of observations.

Matching and potential outcomes

If you remember from the module on potential outcomes, we saw that it’s impossible to see all potential outcomes at once for each person. One of the potential outcomes is always missing for every subject. We can’t see a person’s outcomes in a world under treatment and the outcome of that same person in a world under no treatment without a multiverse or godly knowledge.

In the job training study, for subjects who enrolled in the program, we defined their counterfactual outcome as their outcome had they not received the treatment. Similarly, for those who didn’t enroll in the training program, their counterfactual outcome is their outcome had they received the treatment.

Counterfactual outcomes are not observed. After the treatment decision is made, we only have the observed outcomes $Y^D$.

• If for a person i $D_i=0$, then ${Y_i}^0$ is the observed outcome for that person.
• If for a person i $D_i=1$, then ${Y_i}^1$ is the observed outcome for that person.

However,

• If for a person i $D_i=0$, then ${Y_i}^1$ is the counterfactual outcome for that person.
• If for a person i $D_i=1$, then ${Y_i}^0$ is the counterfactual outcome for that person.

We called this problem the “fundamental problem of causal inference.”

Ok! Enough of reminding you of the things we’ve already discussed. What does matching have to do with the fundamental problem of causal inference?

Assume in a study that we use matching to find matches in the control group for every treated subject in the sample based on the confounders. A control subject that is well matched to a treated subject can be considered its clone or doppelgänger. It’s as if the control unit’s observed outcome is the counterfactual outcome of the treated unit that we can’t normally observe.

Matching fills the gap and provides us with stand-ins for each matched treated unit’s unobserved potential outcomes. As a result, we can compare the potential outcomes under treatment to the potential outcomes under no treatment. And this is how we can estimate the causal effect.

This is why matching, under certain assumptions, and if done correctly, helps us overcome the fundamental problem of causal inference and estimate causal effects.