Some final thoughts on DAGs

As we discussed, the main advantage of DAGs is that they make our assumptions explicit. Without DAGs and without specifying how observed and unobserved variables in a study are related, the researcher still needs to make some assumptions as to how the variables are causally related but chooses not to disclose them.

DAGs aren’t always as simple as the ones we showed!

Sometimes, DAGs include many many nodes and paths. The following DAG shows the causal effects of early life-course factors on caries, a disease that affects teeth in children, from a paper by Birungi et al. 🤯 🤯

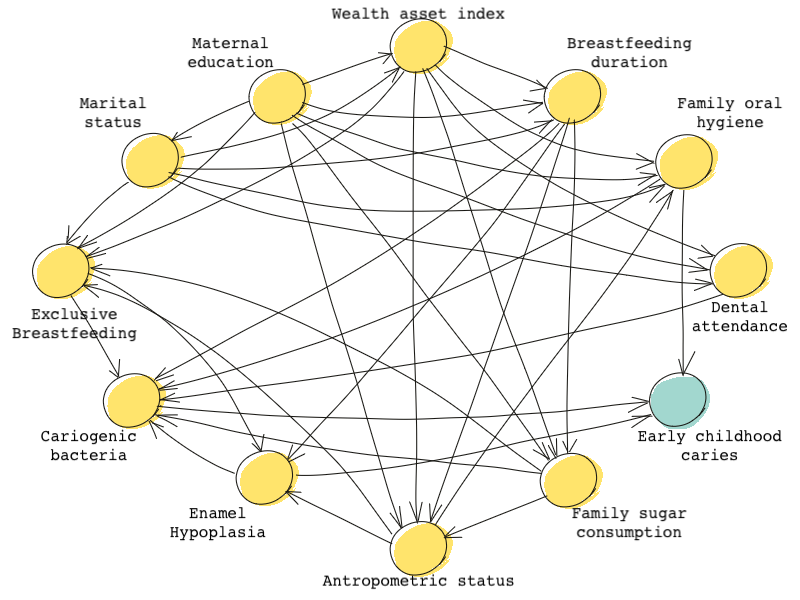
Paths in complex DAGs such as these are not always easy to grasp visually. However, even in a complex causal problem, DAGs can help us understand what variables affect the treatment and the outcomes and whether or not each of these variables needs to be controlled for. DAGs are usually determined and drawn using intuition and prior research. Intuition may tell us that maternal education affects family sugar consumption but we may know from prior scientific research that sugar consumption affects oral hygiene.

In DAGs, missing arrows (the arrows that are intentionally not drawn) are just as important. Their absence reflects the researchers’ assumptions. No arrow between any two variables means that the research has assumed no direct causal relationship between those two variables.

We should note that a DAG is only as good as the assumptions behind it. No DAG should be taken at face value. We can only use our informed-reason to judge whether or not a DAG adequately represents a causal problem.

What if we can’t construct a DAG for our causal problem?

We learned that DAGs can help us identify what to control for and what not to control for in our analysis. But what if it’s hard to come up with a comprehensive DAG for a causal problem? What if it’s impossible to think about all the relevant variables? How do we identify the variables to condition on for finding unbiased causal estimates?

VanderWeele and Shpitser (2011) have introduced a criterion for finding the sufficient set of variables to control for called the disjunctive cause criterion. In this method, when the entire DAG isn’t available, the researcher should block all observed variables that directly cause the treatment, the outcome, or both and control for them.

Imagine a causal setup in which we don’t really know much about the underlying DAG. There are some observed variables $X_1$, $X_2$, $X_3$, the treatment $D$, and the outcome $Y$. Suppose we know this much:

• $X_1$ is a cause of $D$ and a cause of $Y$,
• $X_2$ is neither a cause of $D$ nor of $Y$,
• and $X_3$ is a cause of $D$ but it is not a cause of $Y$.

We know we can’t just simply control for all of the variables as this could open some backdoor paths and cause bias. The common-cause criterion for finding confounders tells us that we should only control for $X_1$, but again this may be naive and cause biases. We also can’t use the backdoor criterion for finding confounders simply because the DAG isn’t available.

This is why disjunctive cause criterion can be useful. The disjunctive cause criterion tells us that we should control for any direct causes of the treatment or the outcome. Therefore, the best set of variables to control for would be $\{X_1, X_3\}$ since $X_2$ is neither a cause for the treatment nor the outcome.

The logic behind this criterion is that if any subset of observed covariates suffices to block all backdoor paths from the treatment to the outcome, then the subset selected by the disjunctive cause criterion will also suffice and will control for the confounding effects.

The disjunctive cause method is very simple but only works if we can identify all the direct causes of the treatment and the outcome.

What now?

In this module, we learned about DAGs and how they can help us identify covariates to control for in order to satisfy the ignorability assumption.

Now that we have the set of covariates to control for, matching and inverse probability weighting are two methods we can use to infer causal inference. In the next module, we will discuss these methods.