Backdoor criterion

You’ve already learned how to block a path. If a path does not contain a collider, controlling for any node (variable) in the middle of the path will shut it. If the path contains a collider, the path is already shut, and controlling for the collider node only opens it up and introduces a new confounding variable (which is not what we want).

So given a DAG, we first identify all backdoor paths and then identify a set of covariates (nodes) that if we control for them will block all backdoor paths. There’s a systematic way of identifying these nodes. This process is called d-separation.

D-separation

Two nodes $D$ and $Y$ are d-separated by a set of nodes (let’s call this set $M$) if conditioning on the nodes in $M$ blocks every path from the treatment $D$ to the outcome $Y$. In mathematical terms:

The symbol $\perp$ here is what denotes the d-separation. If you recall, this notation looks a lot like what we used for the ignorability assumption in the lesson on causal assumptions. Remember, the ignorability assumption dictates that the treatment variable is independent of the outcomes (potential outcomes) conditional on a set of variables X:

Therefore, controlling for the set of variables in $M$ satisfies the ignorability assumption.

Backdoor criterion

So how do we find the set of variables $M$ that would block every path from the treatment to the outcome and satisfy the ignorability assumption? We use the backdoor path criterion. The set of variables $M$ must satisfy the following three criteria:

• $M$ should not include any variables that are descendents of the treatment $D$
• If the backdoor path between the treatment and the outcome contains a chain or a fork, the chain is blocked by including at least one of the middle nodes of the chain
• If the backdoor path between the treatment and the outcome contains a collider, the collider node and its descendants are not included to prevent opening the path (collider paths are automatically blocked)

The first criterion ensures that we do not block any descendents of the treatment $D$ since doing so would erase some of the causal effect of the treatment on the outcome.

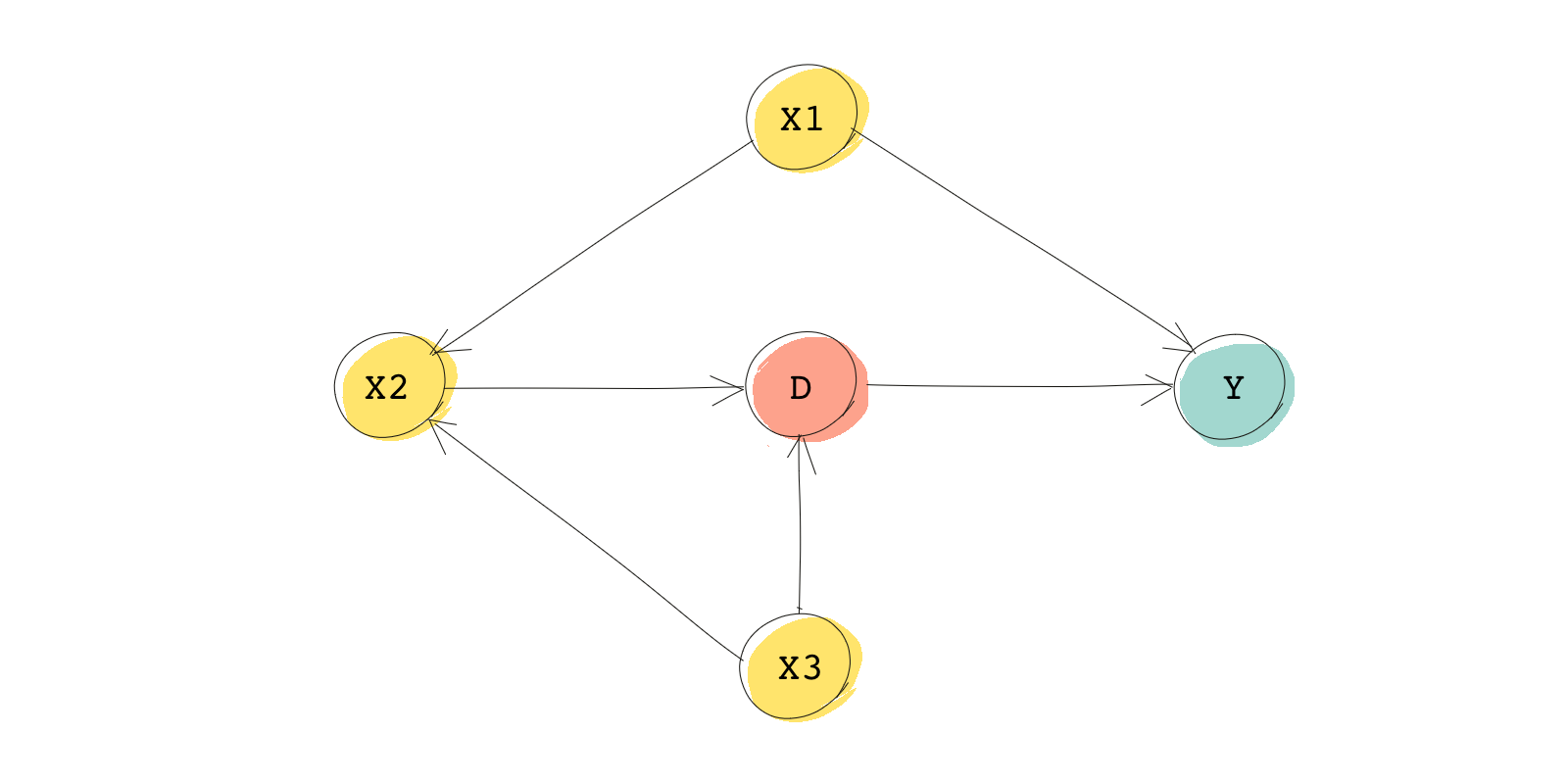
It’s important to note that the set of variables that satisfies the backdoor criterion isn’t unique (in other words, there can be multiple sets of $M$ that will satisfy the condition). Let’s see this through a simple DAG shown below:

To find sets of $M$, we start by identifying all backdoor paths. In this case, there is only one backdoor path which is $D \longleftarrow X_2 \longrightarrow X_1 \longrightarrow Y$. Because there’s no collider in the path, it’s not automatically blocked. To block the path we can either control for $X_1$, $X_2$, or both. Therefore, it is sufficient to control for any one of the sets below:

• $\{X_1\}$
• $\{X_2\}$
• $\{X_1, X_2\}$

Choosing which set to control for is up to you as the researcher, especially if you’re designing a causal study before collecting data, or the set that contains variables for which data is readily available.

Practice

Consider the following DAG. What node is a collider on the backdoor path?

$X_1$

$X_2$

$X_3$

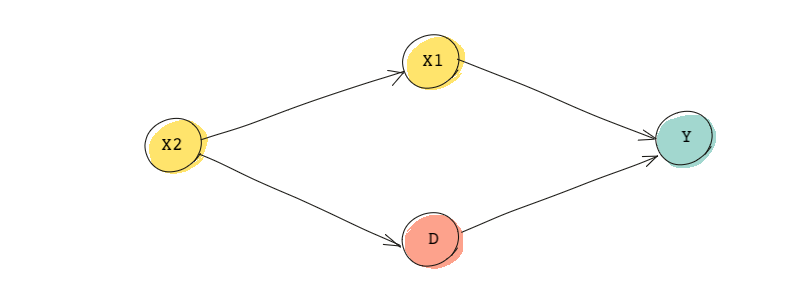
In the DAG above, the backdoor path is simply $D \longleftarrow X_1 \longrightarrow X_2 \longleftarrow X_3 \longrightarrow Y$. This path contains a collider, which means the path is already blocked and there is no confounding. So we can choose not to control for any of the variables and still be able to find the causal relationship between $D$ and $Y$. If for any reason (say accidentally) we control for the collider $X_2$, and open the path, we will have to make sure to control for additional variables to block the path again. For instance, we can control for both $X_2$ and $X_3$ to make sure the backdoor path remains blocked.

We can choose any of the sets $M$ below to control for if we want to find the causal effect of $D$ on $Y$:

• $\{\}$, which is an empty set and means we don’t have to control for anything
• $\{X_1\}$
• $\{X_3\}$,
• $\{X_1, X_3\}$,
• $\{X_1, X_2\}$,
• $\{X_2, X_3\}$,
• or $\{X_1, X_2, X_3\}$.

And because you asked for it, here is a more complicated DAG:

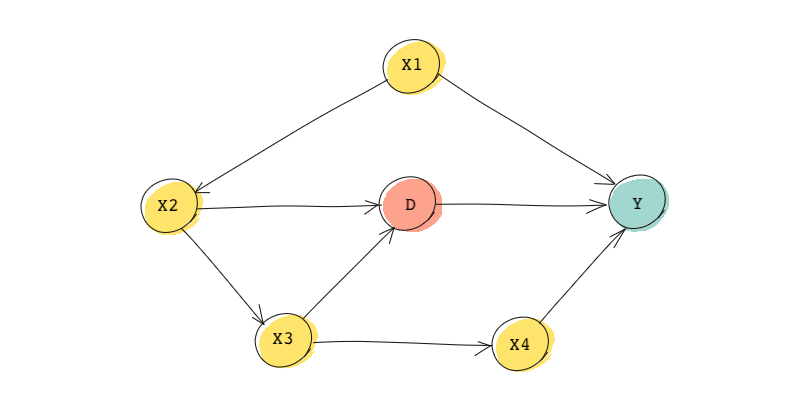
There are three backdoor paths in this DAG. Without looking at the answer below, can you tell what they are?

The following are the backdoor paths and the sets of nodes that would block them:

• $D \longleftarrow X_2 \longleftarrow X_1 \longrightarrow Y$, we need to block $\{X_1\}$, or $\{X_2\}$
• $D \longleftarrow X_2 \longrightarrow X_3 \longrightarrow X_4 \longrightarrow Y$, we need to block $\{X_2\}$, $\{X_3\}$, or $\{X_4\}$
• $D \longleftarrow X_3 \longleftarrow X_2 \longleftarrow X_1 \longrightarrow Y$, we need to block $\{X_1\}$, $\{X_2\}$, or $\{X_3\}$
• $D \longleftarrow X_3 \longrightarrow X_4 \longrightarrow Y$, we need to block $\{X_3\}$, or $\{X_4\}$.

Remember that we need to block all backdoor paths. What set then would block all backdoor paths? Here’s an option: If we control for $X_2$ and $X_3$, all backdoor paths are blocked. This is because controlling for $X_2$ blocks the first and the second backdoor paths and controlling for $X_3$ blocks the third one. So a possible set would be $\{X_2, X_3\}$. However, there are other (minimal) sets that if we control for them, all backdoor paths will be blocked.

• $\{X_2, X_3\}$
• $\{X_1, X_3\}$
• $\{X_2, X_4\}$
• $\{X_1, X_4\}$

We call these minimal sets because obviously we can control for $\{X_1, X_2, X_3\}$ to block all paths or even control for all variables $\{X_1, X_2, X_3, X_4\}$.

Practice

Consider the DAG below! What single variable, if controlled for, blocks all backdoor paths between the treatment, $D$, and the outcome, $Y$?

$X_1$

$X_2$

$X_3$

None