Collider bias

Collider bias

We saw in the previous lesson that rather than controlling for all of the variables that fit the common-cause criteria for a confounder, we only need to control for a subset of these variables $M$ such that all backdoor paths from the treatment to the outcome are blocked.

In a simple DAG, confounders found through the common-cause criteria and those that satisfy the backdoor criterion may end up being the same. For instance, let’s go over the DAG shown below:

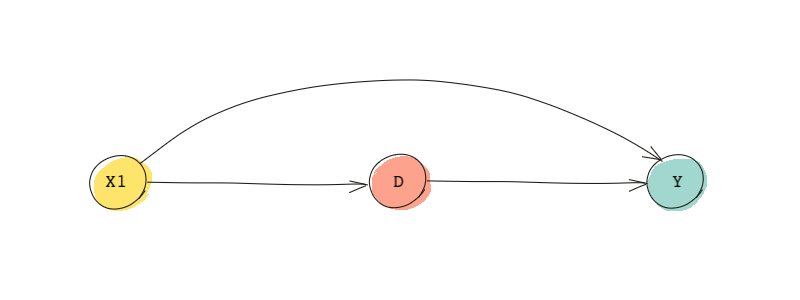
As we discussed, $X_1$ is associated with the treatment, and it is associated with the outcome, and, therefore, is a confounder. Using the backdoor criterion, too, we reach the conclusion that $X_1$ needs to be controlled for in order to block the backdoor path.

However, controlling for the traditionally-defined confounders may lead to inappropriate adjustments. We will see that the backdoor criterion is more reliable in determining what needs to be controlled for. Consider the following DAG:

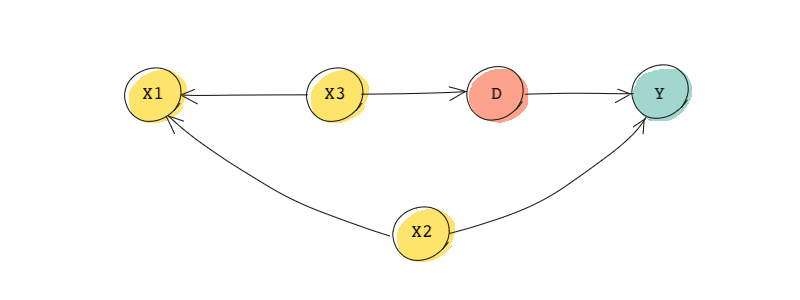
We know that $X_1$ is associated with the treatment (through $X_3$), and it is associated with the outcome (through $X_2$). So it meets the common cause criteria for finding a confounder.

However, as we know from the backdoor criterion, controlling for $X_1$, would bias the estimator because it opens up the backdoor path since it’s a collider. Therefore, in this example, if we only control for $X_1$, we introduce bias. The backdoor criterion tells us that we don’t need to control for any of the variables $X_1$, $X_2$, and $X_3$ as the backdoor path is already blocked.

The bias caused by (usually inadvertently) controlling for a collider is simply called the collider bias. Collider bias is one one of the reasons DAGs have become more popular in recent years simply because DAGs can help us identify them.

The traditional approach to finding covariates to control for to satisfy the ignorability assumption may be misleading. A better approach is to control for covariates that block all backdoor paths between the treatment and the outcome.

Example one: Are older people happier?

To get a grasp of what collider bias is, think about the following causal question: The causal effect of age on happiness. The data collected from a sample of 1,000 individuals shows no clear causal effect of age on happiness as shown below.

However, a researcher suspects that marital status is a potential confounder and should be controlled for; it is suspected that it is associated with both the treatment (age) and the outcome (happiness).

When the researcher controls for happiness (e.g., separates the analysis for married and unmarried individuals according to the following graph), she finds a negative causal relationship between the treatment and the outcome.

Which result should we trust?

A DAG would be helpful. Assume we know that age directly affects happiness, age affects marital status (older people are more likely to be married), and happiness affects the probability of being married (ok, there’s no proof for this, but let’s just assume). Then the following DAG represents our problem:

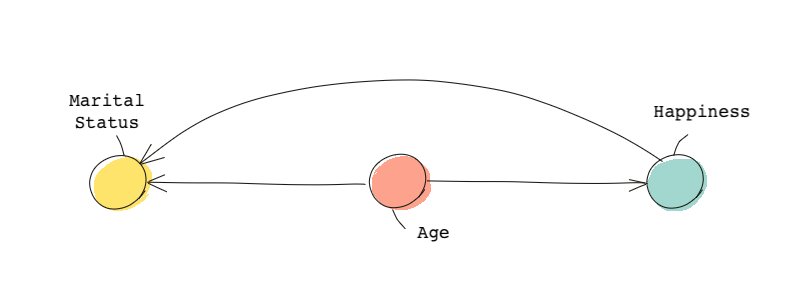
Our treatment (age) directly affects happiness and there is one backdoor path: age $\longrightarrow$ marital status $\longleftarrow$ happiness.

Because we’re only interested in the direct effect of age on happiness and not in any other indirect channel, we need to make sure the backdoor path is blocked. But marital status seems to be a collider because both arrows from age and happiness are toward marital status. As a result, the path is automatically blocked and we don’t need to control for anything.

When the researcher controls for marital status, she opens up the indirect effect of age on happiness through marriage, which will create collider bias and bias the results.

Example two: SAT scores and siblings

A researcher at Harvard University is interested in the relationship between SAT score and the number of siblings. He runs a survey of students at Harvard and ask them about their SAT score and how many siblings they have. At the end of the survey, he finds that fewer siblings means higher SAT scores.

What’s going on? The answer lies in the existence of a collider. The graphs only represents those who are admitted to Harvard University and not everyone including students outside of Harvard. From intuition we know the following DAG represents the situation:

In other words, a higher SAT score increases the chances fo getting into Harvard. At the same time, if a person has more siblings, it means they are more likely to have a sibling with connection to Harvard and, for the sake of our example, assume that increases a prospective students’ chances of getting into Harvard (aka legacy admissions, sigh). Admission to Harvard seems to be a collider in the DAG shown above because both number of siblings and SAT scores collide in it. Therefore, we know SAT score and the number of siblings should be automatically independent of each other.

However, when the researcher looks only at Harvard students as the source of his data, he is conditioning on being admitted to Harvard. Conditioning on the collider, opens the path between the number of siblings and SAT scores and as such creates dependence between the two variables. This is why, the researcher sees a negative relationship between SAT scores and the number of siblings in the data.