Chains, forks, and colliders

This lesson is all about paths. You’ve already learned what paths are and how to differentiate between direct and indirect paths. In this lesson, you’ll learn to identify three distinct types of paths: chains, forks, and colliders. These are the basic building blocks of any DAG, and they contain only three nodes.

In future lessons, you’ll learn to see that any DAG is just a constellation of these three basic path patterns. Learning to identify chains, forks, and colliders within a more complicated DAG and understanding the implications of each pattern is a fundamental skill for this course.

Chains (Pipes)

A chain (also referred to as a pipe) is a path containing three nodes that takes you from the first node to the third node without changing direction. In the DAG below, you can go from $X_1$ to $X_2$ to $X_3$ without changing direction (i.e., all of the arrows are pointing in the same direction). The variable that sits in the middle of a chain is called the mediator.

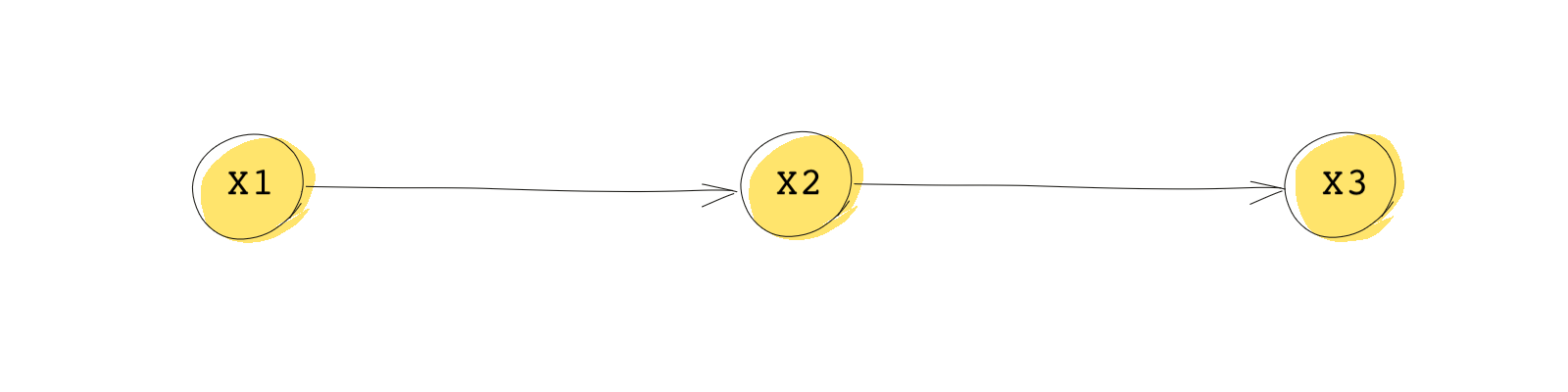
Let’s consider a conceptual example of a chain where $X_1$ is inches of rain in an hour, $X_2$ is the number of rides a Lyft driver gets in an hour, and $X_3$ is the income earned by the driver in that hour. If there is heavy rain one afternoon, we can expect the following sequence of events: more people will want to take a Lyft, so the driver gets more rides, and the more rides the driver gives, the higher the driver’s income will be. Here, $X_1$ causes $X_2$, and $X_2$ causes $X_3$, but rain is not a direct cause of the driver’s income. It’s an indirect cause. The significance of a chain is that if we condition on the mediator $X_2$, then $X_1$ and $X_3$ become independent. In plain English, if we have information about $X_2$, we do not need to know anything about $X_1$ to make inferences about $X_3$. If we know the driver got more rides, we don’t need to know anything about the weather, to make inferences about income.

Mathematically, this all looks and sounds much more complicated: the probability of $X_3$ conditional on both $X_1$ and $X_2$ is equal to the probability of $X_3$ conditional only on $X_2$.

Forks

In a fork, one node is the common cause of the other two nodes. In the fork below, $X_2$ is the common cause of both $X_1$ and $X_3$.

As an example, think of $X_2$ as the average income of a country, $X_1$ as chocolate consumption in said country, and $X_3$ as the number of Nobel laureates from that country. This is a famous example that you may have encountered in other courses.

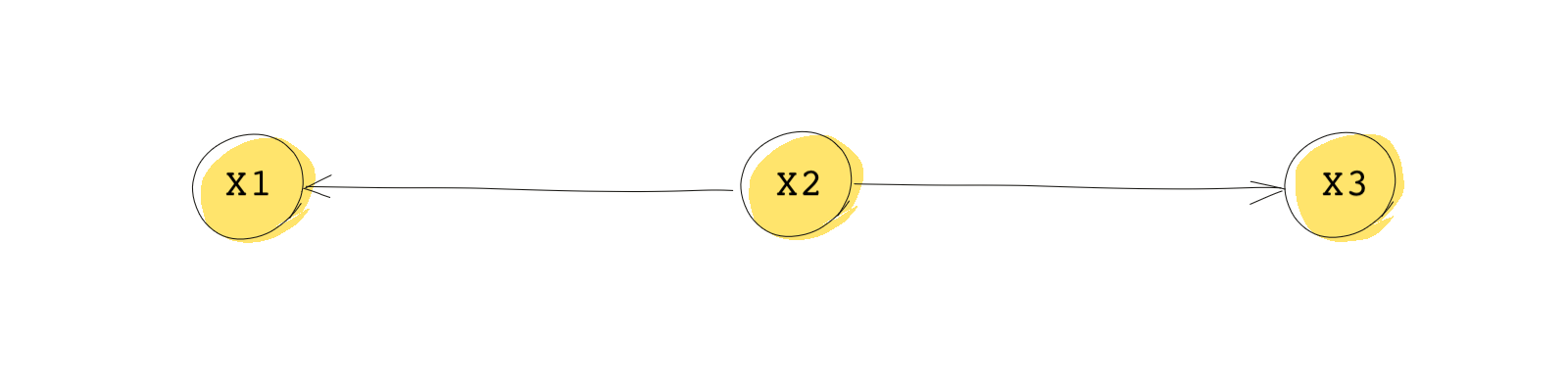
This DAG shows that $X_3$ and $X_1$ are not independent because the same information flows to both of them. However, $X_3$ and $X_1$ will be independent if we condition on $X_2$.

When thinking about our example this becomes even clearer. If you look at the relationship between chocolate consumption and the number of Nobel Laureates in a country, you find a surprisingly strong correlation (the variables are not independent). This intrigued some researchers and even led a group of medical experts to the following hypothesis: eating chocolate increases cognitive function, which then helps to explain the high number of Nobel laureates in countries where chocolate consumption is high. Notice that this hypothesis would be represented by a chain leading from chocolate consumption to Nobel Laureates with cognitive function acting as the mediator.

But there’s a simpler and likely more reasonable explanation represented, which can be represented by a fork. Chocolate consumption and Nobel laureates share a common cause: how rich a country is. The richer people are in a country, the more likely they are to consume chocolate; the richer people are in a country, the more likely the country is to produce Nobel Laureates. The fork pattern suggests that controlling for $X_2$ should make the other two variables independent (i.e, if you were to look within specific countries you would observe no relationship between chocolate consumption and the likelihood of winning a Nobel Prize.

Mathematically, we can say:

Colliders (Inverted forks)

A collider (sometimes called an Inverted fork) is the opposite of a fork. In a collider, two nodes are each a direct cause of the third node. In the DAG below, $X_1$ and $X_2$ are both causes (a parent) of $X_3$.

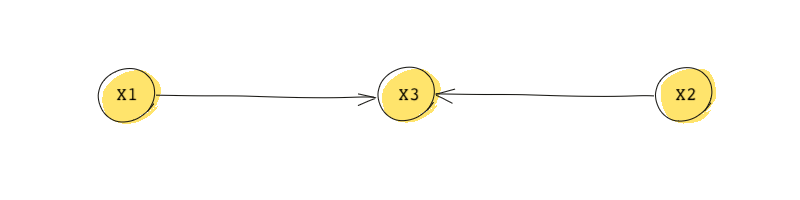
Note here that $X_1$ and $X_2$ are independent. This is because there is no flow of information from one to the other. Besides they don’t receive the same information. In some ways, the information flow between $X_1$ to $X_2$ collides in $X_3$ and that’s why $X_3$ is called a collider.

In the DAG above, however, if we condition on $X_3$, they become dependent. This is very important and we’ll come back to it in the next lesson. If we unintentionally condition on a collider (thinking we’re removing confounding), we may actually introduce confounding in our analysis.

Imagine we want to estimate the effect of class attendance on academic outcomes (like grades). We know (at least for the sake of our example) that those who attend classes learn more, and therefore, perform better on exams. We also know that the professor of the class we’re talking about has dedicated a portion of her students’ overall grade to class attendance, hence attendance also directly affects grades. What do you think the DAG for this example will look like?

You’re absolutely right! It looks something like this:

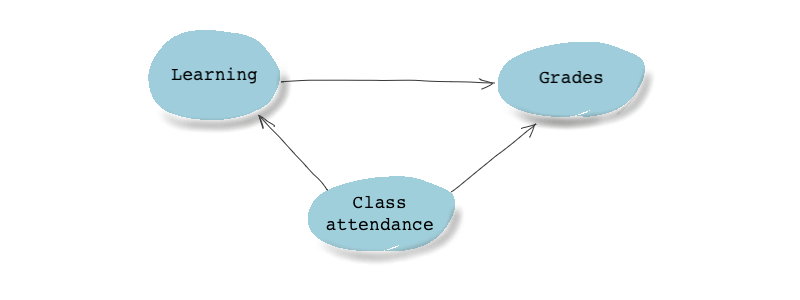
This DAG doesn’t really look like any of the path types we just saw, but look closely and you’ll see that there are two paths between the treatment (class attendance) and the outcome (grades).

• It has a direct path in it: Class attendance $\longrightarrow$ Grades.
• And it also has a chain: Class attendance $\longrightarrow$ Learning $\longrightarrow$ Grades.