Synthetic control

Matching (and weighting) methods are extremely useful methods for improving causal estimates so long as the ignorability assumption is satisfied. These methods rely on an assumption that we usually don’t bother to check because in other cases it’s usually not an issue. When matching and weighting are deployed, we need to make sure that there are “enough” observations in both the treatment and the control groups.

If there are not enough observations in each group, causal estimates won’t improve much from just using linear regression. You’d be surprised to know that there are, however, causal questions where there is only one treated subject. Here’s an example from a recent paper.

In the early 1990s, Sweden (🇸🇪) introduced a carbon tax on transport fuels. It was one of the first countries in the world to impose such a tax. When it was first introduced, the tax was set at 30 US dollars per ton of CO2, and since then the tax has increased to 132 dollars per ton. The tax is now considered the highest carbon tax in the world.

Researcher Julius Andersson was interested in understanding the causal effect of Sweden’s carbon tax on carbon emissions. If the effects were large enough, it would be worthwhile to recommend such a policy to other countries.

Where was Andersson to start? Clearly, he was dealing with observational data. A simple before and after comparison wouldn’t be convincing since there were countless other factors that could have impacted the environment in the periods before and after the policy was introduced. This would make it difficult to isolate the causal effect of the tax.

Not only that. He was dealing with a treatment group with only one treated subject: 🇸🇪. Because, there’s only one treated unit, the typical over-the-counter tools we’ve looked at so far such as matching, IPW, or regression analysis are off the table. What to do then?

In an upcoming lesson, we’ll look at a method called difference-in-differences (DID). DID might be useful in this case, but it requires several strict assumptions. In this lesson, we’ll use a method called the synthetic control method.

The synthetic control method is used to create a “synthetic” (or artificial) control group when no perfect control group actually exists. The idea is to weight control observations to make a single ensemble control unit that can provide the counterfactual outcome for our treatment subject.

In our example, let’s just focus on Europe. If there are 10 countries in Europe that didn’t implement a carbon tax in the 1990s, then we can use them to build a single control subject to estimate the causal effect of the carbon tax in 🇸🇪. Our synthetic control is like a stew 🥣 . It has a little bit of Norway, a little of Denmark, a pinch of France and the UK, etc.

Once we build this synthetic control, we can then use it as a counterfactual for 🇸🇪, i.e., the synthetic control subject would represent what would have happened in 🇸🇪 had it not implemented the policy. Let’s call this synthetic control unit “Synthetic Sweden.” We can then easily compare the real 🇸🇪 to Synthetic Sweden to estimate the causal effect.

A perfect synthetic control setup

Synthetic control is similar to matching and IPW. These are some of the main characteristics of a synthetic control dataset.

1. Similar to matching and IPW, the data need to provide us with a satisfactory set of covariates for sound causal estimation. Julius Andersson’s study uses GDP per capita, the number of motor vehicles, gasoline consumption per capita, and the percentage of urban population as key covariates.
2. We need to have a set of reasonable potential control subjects. This set of control subjects is usually called the donor pool. For instance, making a synthetic 🇸🇪 out of a group of developing countries is not a great idea, because they would be too different from Sweden across too many variables.
3. In addition, the units in the donor pool cannot be treated during the study period. In the 🇸🇪 paper, Andersson excludes countries that enacted carbon taxes in the transport sector during the sample period (Finland, Norway, and the Netherlands) and countries that made large changes to fuel tax (Germany, Italy, and the UK). We should also drop units from the donor pool that have witnessed large idiosyncratic shocks in their outcome variable during the study period if those shocks would have not affected the treated unit in the absence of the treatment. Remember, the goal is always to get the treatment and control groups to be as similar as possible.
4. Unlike matching and weighting, the data need to be from multiple time periods. In fact, the weights on the control subjects are calculated based on their pre-treatment trends. The pre-treatment time trends then need to be long enough for good weight calculation. The synthetic control method is a before-after-treatment analysis and as such requires data from both before and after the treatment for the treated and the control subjects.
5. There shouldn’t be the possibility of spillover effects, i.e., the treatment on the treated should not affect the control units. As a hypothetical example, if the tax policy imposition made Swedish drivers fill their tanks in Denmark, this assumption is violated.

The synthetic control procedure

The data should include the covariates for the donor pool units and the treated unit. Once we have the data, the algorithm helps create a synthetic control subject that is a weighted average of the donor control subjects.

The algorithm for finding the weights is based on the objective of making the pre-treatment covariates trends of the synthetic control unit similar to the pre-treatment covariates trends of the treatment unit. If the pre-treatment covariates in the synthetic control are similar to those in the treated subject, then the pre-treatment outcomes should be similar as well (if there are no unobserved confounding, however).

So in the above example, the weights are chosen so that the trends in the key confounding variables for Synthetic Sweden are similar to the trends in real 🇸🇪. Mathematically, the objective is to minimize the difference in trends. If the trends in covariates are similar, then the pre-treatment pollution rate in Synthetic Sweden should be similar to the pre-treatment pollution rate in real 🇸🇪.

You love math and we know it. So let’s get to it 😄

Imagine we have $J$ control subjects in the donor pool. We can denote the vector of weights that we’re about to find for the control subjects by $W$. The transposed version of the vector can then be written as:

where $w_j$ denotes the weight of control unit $j$. These weights should sum to 1. Thus, $w_1+w_2+ ... + w_J = 1$. If we find a weight of 0.1 for 🇧🇪, it means that the contribution of 🇧🇪 to Synthetic Sweden is 10 percent.

Let’s say we have $K$ covariates and that the vector $X^{\text{treated}}$ stores the pre-treatment value of those covariates for the one treatment unit we have. Therefore, $X^{\text{treated}}$ is a $K \times 1$ vector. We say pre-treatment because we find weights using only the pre-treatment values of the covariates.

For the pre-treatment value of the covariates for the donor pool, we define $X^{\text{donor pool}}$ but this vector is $K \times J$ because there are $K$ covariates and $J$ donor control units.

One last piece of notation. Let’s define $V$ as a matrix reflecting the relative importance of the different covariates. This matrix is $K \times K$ and is a diagonal matrix where all non-diagonal elements of the matrix are zero.

Mathematically, the weights are calculated so that the following objective function is minimized:

You can think of this as the squared distance between the value of covariates for the treatment unit and the value of covariates for the synthetic (weighted) control unit. Let’s say the vector of weights that minimizes the objective function above is $W^*$.

A little note about the vector $V$. We said that this vector represents the relative importance of each covariate in our analysis. For instance, if GDP per capita is our most important covariate, we would like to assign a high value for the element representing GDP per capita. So the values of this vector could be based on our intuition or prior knowledge.

But, we could also choose the values of the vector $V$ to make sure the pre-treatment outcome trend for the synthetic control unit matches the pre-treatment outcome trend for the treated unit. In our example, we choose vector $V$ so that the pre-1990 trend in pollution for the synthetic 🇸🇪 is most similar to the pre-1990 trend in pollution for 🇸🇪. So instead of our intuition, we let the data dictate the value of this vector to us.

Our goal is then to find the vector of weights $W$ given that we have $X^{\text{treated}}$ and $X^{\text{donor pool}}$. Andersson found the weights for each of the 24 countries in the donor pool as follows. Not so surprisingly, Denmark (🇩🇰) has the highest weight of 0.48. This means the contribution of 🇩🇰 to Synthetic Sweden is 48 percent and 🇩🇰 is the closest country in terms of the pre-treatment covariates to 🇸🇪. The next country is 🇳🇿 with weight 0.17 followed by 🇬🇧 with weight 0.13 and then 🇧🇪 with weight 0.1. The rest of the countries in the donor pool have small weights.

This is not what we’re really after but we can calculate the value of the covariates for the synthetic control unit by calculating:

Here, we’re weighing the covariates by their weights.

After we find the weights, estimating the causal effect is easy. We just have to calculate the difference between the potential outcome under treatment and the potential outcome under no treatment. The potential outcome under treatment is observed and is the outcome vector for the treated unit. Let’s call it $Y^{\text{treated}}$. This vector is $T \times 1$ for the $T$ time periods in the study.

The potential outcome under no treatment is the potential outcome of the synthetic control unit which we estimate. Let’s call it $Y^{\text{synthetic}}$ and is also a $T \times 1$ vector. It can be estimated as:

Therefore, $Y^{\text{synthetic}}$ is a weighted average of the outcomes of the donor pool. $Y^{\text{donor pool}}$ is $T \times J$ matrix because we have $J$ units in the donor pool and $T$ time periods. If we have both $Y^{\text{treated}}$ and $Y^{\text{synthetic}}$, we can plot them against each other. Something like this:

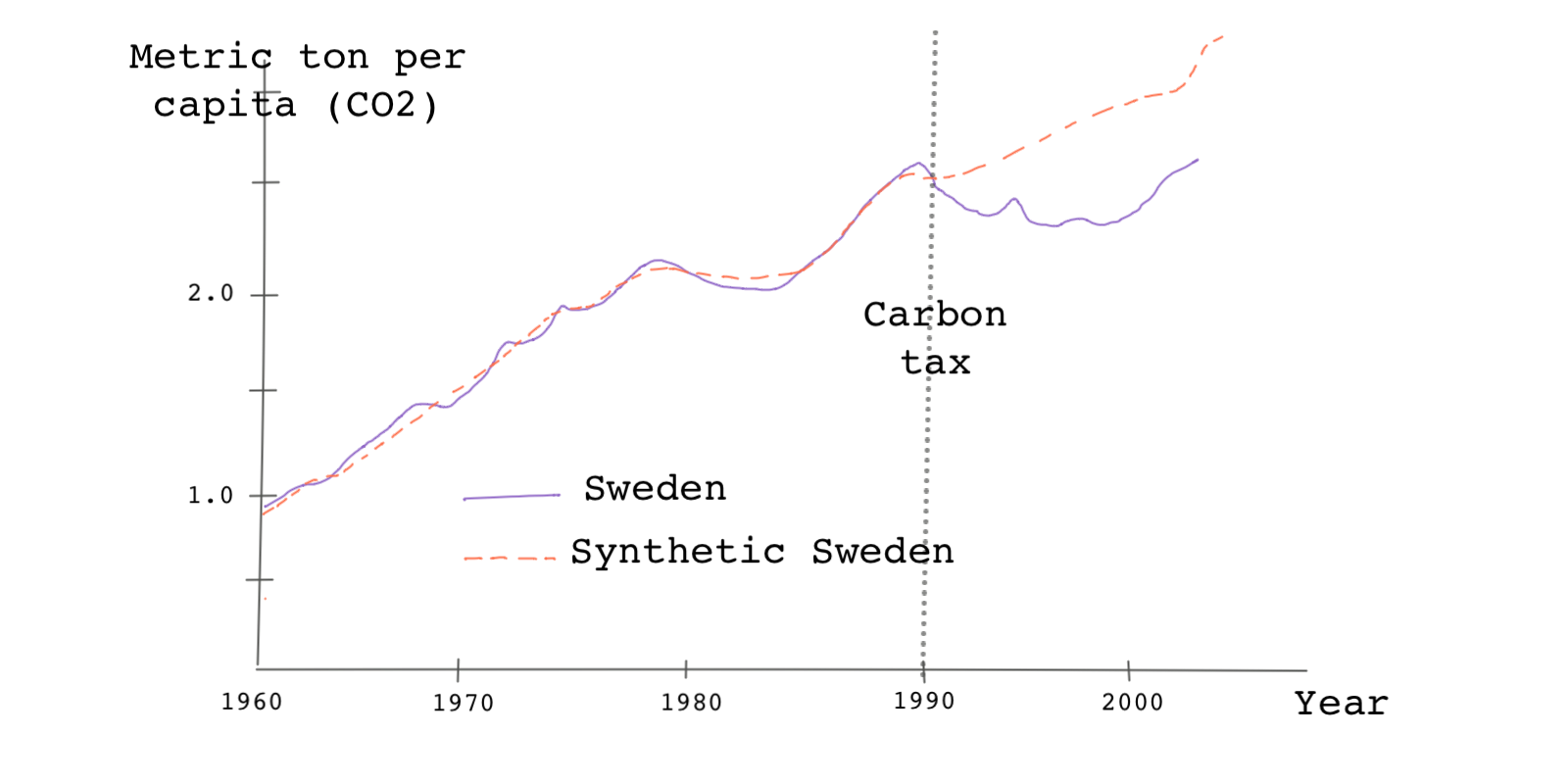
Ideally, we want the pre-treatment trends to be as similar as possible because the assumption is that the synthetic unit is similar to the treated unit in every aspect except the treatment assignment. We can, therefore, attribute the post-treatment differences between the two trends to the treatment effect. In this case, we attribute the difference between the outcomes after 1990 to the carbon tax policy. As we can see, after the introduction of the policy, the pollution rate in 🇸🇪 diverges from its synthetic counterpart. Emissions in real 🇸🇪 were less than in Synthetic Sweden post-treatment, so we can conclude the policy has been effective in reducing emissions.

To sum up the whole process, this is what we do in synthetic control:

• Find weights that minimize $(X^{\text{treated}} - X^{\text{donor pool}} W)^T V (X^{\text{treated}} - X^{\text{donor pool}} W)$
• Find the covariate trend for the synthetic control as $X^{\text{synthetic}} = X^{\text{donor pool}} W^*$
• Find the outcome of the synthetic control unit as $Y^{\text{synthetic}} = Y^{\text{donor pool}} W^*$
• Calculate the estimated treatment effect at each time period by taking $Y^{\text{treated}} - Y^{\text{synthetic}}$

Synthetic control analysis can be easily done in most statistical software. Let’s first import the data from Andersson’s paper on carbon tax policy. You can read about the data here.

rpythonstata

# Let's load the data from the web link.
# The data is in the form of a dataframe. 
tax_policy <- read.csv("https://bit.ly/andersson_taxpolicy", stringsAsFactors=FALSE)

rpythonstata

import pandas as pd
 
# Now, let's load the mortality data
tax_policy = pd.read_csv("https://bit.ly/andersson_taxpolicy")

rpythonstata

* Let's load the data from the web link.
import delimited https://bit.ly/andersson_taxpolicy

The data is in the form of a matrix (data.frame) and not a panel dataset. A panel dataset is a form of data that helps us better work with data from various units over a time interval. Let’s do that first.

rpythonstata

# For synthetic control analysis in R, we can use the Synth package.
# If you haven't installed the package already, you can install it by
# running the command install.package("Synth")
# Now, we can load the package
library(Synth)

# The synth() function we're going to use next takes a standard panel dataset.
# So we first need to change the dataframe into a panel dataset by using the 
# function dataprep().
# The 'foo' argument takes the dataset. 
# The 'predictors' argument takes the vector of all predictors. 
# The argument 'predictors.op' can take different methods used for matching 
# predictors. If we use 'mean', we use mean of the predictors.
# If there are any additional numeric predictors, we feed them into the argument
# 'special.predictors'. Here we are using the pre-treatment values of the outcome
# variable as well. 
# We then have to define the dependent variables using the argument 'dependent'. 
# Our dependent variable is CO2 emissons per capital from transportation.
# In argument 'unit.variable' we enter the column number or the column name 
# of the column that identifies the donor pool unit numbers. 
# The argument 'unit.names.variable' takes the column number or the column name 
# of the column that identifies the donor pool unit names.
# The argument 'time.variable' takes the column number or the column name of the
# column that represents time periods.
# So far we haven't told the function which unit is our treatment unit. We can 
# do that using the argument 'treatment.identifier'. Unit 13 is Sweden. 
# The rest of the units are the control units. We define them using the argument
# 'controls.identifier'. 
# 'time.optimize.ssr' defines the periods of the time interval over which we want
# minimze the objective function. This is usually set at the pre-treatment time
# interval. Finally, 'time.plot' is the argument that sets the time interval over
# which the results of the analysis are to be plotted. This usually is both the
# pre-treatment and post-treatment time intervals combined. 
dataprep.out <-
    dataprep(foo = carbontax,
             predictors = c("gdp_per_capita" , "gas_cons_capita" , "vehicles_capita" ,
                            "urban_pop") ,
             predictors.op = "mean" ,
             time.predictors.prior = 1980:1989 ,
             special.predictors = list(
                 list("co2_transport_capita" , 1989 , "mean"),
                 list("co2_transport_capita" , 1980 , "mean"),
                 list("co2_transport_capita" , 1970 , "mean")
             ),
             dependent = "co2_transport_capita",
             unit.variable = "countryno",
             unit.names.variable = "country",
             time.variable = "year",
             treatment.identifier = 13,
             controls.identifier = c(1:12, 14:15),
             time.optimize.ssr = 1960:1989,
             time.plot = 1960:2005
    )

rpythonstata

# Make sure you have all the necessary packages installed before running this

import numpy as np 
import pandas as pd 
import statsmodels.api as sm 
import statsmodels.formula.api as smf 
from itertools import combinations 
import plotnine as p
from rpy2.robjects.packages import importr
from rpy2.robjects.conversion import localconverter
Synth = importr('Synth')

control_units = list(range(1, 13)) + list(range(14,16))

robjects.globalenv['tax_policy'] = tax_policy

predictors = robjects.vectors.StrVector(["gdp_per_capita" , "gas_cons_capita" , "vehicles_capita" ,
                            "urban_pop"])
sp = robjects.vectors.ListVector({'1': ['co2_transport_capita', 1989, 'mean'], 
                                  '2': ['co2_transport_capita', 1990, 'mean'], 
                                  '3': ['co2_transport_capita', 1970, 'mean']})

dataprep_out = Synth.dataprep(tax_policy, 
    predictors = predictors,
    predictors_op="mean",
    time_predictors_prior=np.arange(1980, 1990),
    special_predictors=sp,
    dependent='co2_transport_capita',
    unit_variable='countryno',
    unit_names_variable='country',
    time_variable='year',
    treatment_identifier=13,
    controls_identifier=control_units,
    time_optimize_ssr=np.arange(1960, 1990),
    time_plot=np.arange(1960, 2006))

synth_out = Synth.synth(data_prep_obj = dataprep_out)


weights = synth_out.rx['solution.w'][0]
ct_weights = pd.DataFrame({'ct_weights':weights.flatten(), 'countryno':control_units})
ct_weights.head()

tax_policy = pd.merge(ct_weights, tax_policy, how='right', on='countryno')

tax_policy = tax_policy.sort_values('year')
ct = tax_policy.groupby('year').apply(lambda x : np.sum(x['ct_weights']*x['co2_transport_capita']))
treated = tax_policy[tax_policy.countryno==48]['co2_transport_capita'].values
years = tax_policy.year.unique()


plt.plot(years, ct, linestyle='--', color='black', label='control')
plt.plot(years, treated, linestyle='-', color='black', label='treated')
plt.ylabel('co2_transport_capita')
plt.xlabel('Time')
plt.title('Synthetic Control Performance')```

```multi-stata
* The synth command we're going to use next takes a standard panel dataset.
* So we first need to change the data into a panel dataset by using the xtset
command.
xtset countryno year

Now, that the data is ready for analysis, we simply use the appropriate function for calculating the weights.

rpythonstata

# The function synth() helps us find the weights using the algorithm we discussed.
# We have to tell the function what our panel dataset is. 
synth.out <- synth(data.prep.obj = dataprep.out)

# The weigts are stored in the output object. This is how we can retrieve 
# country weights in the synthetic Sweden.
# We can see that Denmark has the highest weight.
synth.tables <- synth.tab(dataprep.res = dataprep.out,
                          synth.res = synth.out
)
synth.tables$tab.w[1:14, ]

rpythonstata

# Python codes will be added soon

rpythonstata

* For synthetic control analysis in Stata, we can use the synth package.
* If you haven't installed the package already, you can install it by
* running the command below
* ssc install synth, replace all

* The first argument is the dependent variable followed by all the predictor
* variables. Our dependent variable is CO2 emissons per capital from transportation.
* Note that we can use the pre-treatment outcome as a predictor 
* as well. If we specify numbers in paranthesis for a specific predictor, we're 
* telling the command to average that predictors only across the years specified.
* The argument trunit specifies which unit number represents the treated unit 
* (here Sweden). The rest of the units are the control units.
* The argument trperiod specifies the year the treatment happened. 
* The argument xperiod allows to specify a common period over which all predictors 
* should be averaged.
* The argument mspeperiod is a list of pre-intervention time periods over which
* the mean squared prediction error (MSPE) should be minimized. This is usually 
* set at the pre-treatment time interval. 
* Finally, the argument resultsperiod is the period over which the results of
* synth should be obtained in the figure. This usually is both the pre-treatment 
* and post-treatment time intervals combined.
synth co2_transport_capita co2_transport_capita(1970) co2_transport_capita(1980) ///
co2_transport_capita(1989) gdp_per_capita gas_cons_capita vehicles_capita urban_pop, ///
trunit(13) trperiod(1990) xperiod(1980(1)1989) mspeperiod(1960(1)1989) ///
resultsperiod(1960(1)2005)

Calculating the weights of the donor pool is the most important step in synthetic control analysis. Once we have them, we can look at the value of the covariates for synthetic Sweden.

This is how:

rpythonstata

# We can also look at the pre-treatment mean of the covariates for 
# the synthetic Sweden and the treated unit. You can see that the values
# are pretty similar indicating that the weights are well-calculated.
synth.tables$tab.pred[1:7, ]

rpythonstata

# Python codes will be added soon

rpythonstata

* The synth command in Stata that we ran above automatically returns the
* balance of the covariates across the treated and the synthetic units. So we don't
* have to run a new command. See above.

And finally, let’s look at the difference between the treated unit (Sweden) and the synthetic unit (Synthetic Sweden). We can use a path plot. Path plots show the pre- and post-treatment trend for the outcome variable for both the treated unit and the synthetic control unit.

rpythonstata

# The package has a function for creating path plots based on the results.
path.plot(synth.res = synth.out,
          dataprep.res = dataprep.out,
          Ylab = "Metric tons per capita (CO2 from transport)",
          Xlab = "Year",
          Ylim = c(0,3),
          Legend = c("Sweden","synthetic Sweden"),
          Legend.position = "bottomright"
)

rpythonstata

# Python codes will be added soon

rpythonstata

* If you simply add 'fig' option at the end of the synth command a path plot
* will automatically be generated
synth co2_transport_capita co2_transport_capita(1970) co2_transport_capita(1980) //
co2_transport_capita(1989) gdp_per_capita gas_cons_capita vehicles_capita urban_pop, ///
trunit(13) trperiod(1990) xperiod(1980(1)1989) mspeperiod(1960(1)1989) ///
resultsperiod(1960(1)2005) fig

If you obtain the path plot, you see that the pre-treatment paths are similar, but after the treatment is introduced, the two trends diverge. We can show this divergence by using what is called a gap plot. A gap plot simply shows the gap between pre-and post-treatment outcome trends for the treated and the synthetic units.

rpythonstata

# The function gap.plot() plots the gaps between the potential outcome of the 
# treated unit and the synthetic unit.
gaps.plot(synth.res = synth.out,
          dataprep.res = dataprep.out,
          Ylab = "Gap in metric tons per capita (CO2 from transport)",
          Xlab = "Year",
          Ylim = c(-0.5,0.5),
          Main = NA
)

rpythonstata

# Python codes will be added soon

rpythonstata

* Let's run the synth command again
synth co2_transport_capita co2_transport_capita(1970) co2_transport_capita(1980) ///
co2_transport_capita(1989) gdp_per_capita gas_cons_capita vehicles_capita urban_pop, ///
trunit(13)trperiod(1990) xperiod(1980(1)1989) mspeperiod(1960(1)1989) resultsperiod(1960(1)2005)

* preserve command in Stata preserves the data, guaranteeing that data
* will be restored after program termination. restore forces a restore of
* the data now.
preserve
* We can then store the difference of the two in matrix a. 
* e(Y_treated) and e(Y_synthetic) contain the values of the dependent variable
* for each time period for the treated and synthetic control units, respectively.
matrix a =  e(Y_treated) - e(Y_synthetic)
svmat double a, name(gap)
keep gap year
drop if gap==.
* Then we can plot the gaps between the potential outcome of the treated unit 
* and the synthetic unit. 
twoway line gap year, ///
yline(0, lpattern(shortdash) lcolor(black))
xline(1990, lpattern(shortdash) lcolor(black)) ///
xtitle("Year",size(medsmall)) xlabel(#10) ///
ytitle("Gap in metric tons per capita (CO2 from transport)", size(medsmall))
* Finally, let's restore the original data
restore

In the next lesson, we’ll go over synthetic control methods in some more detail.