Difference-in-differences method

DiD you know!

The synthetic control method is great for when there are data over time. It’s a straightforward method that is similar in nature to weighting methods, but two challenges stand in the way of using this method:

• If even after weighting, the characteristics of the control units are far from the treated ones, there will be bias in the causal estimates
• The pre-treatment time trends need to be long enough for proper weight calculation. So this method isn’t fit for cases when we only have two points in time.

In most cases, we usually only have their treatment status and their outcomes in two points in time: before treatment and after treatment.

In such cases, we use a different method called the difference-in-differences or DiD method. Let’s go through an example about the minimum wage.

Does an increase in minimum wage reduce employment?

The minimum wage is the lowest compensation that employers can pay their workers. Many countries have minimum wage laws and in some countries, the minimum wage varies by locality. Modern minimum wage laws were first introduced in New Zealand and Australia in the 1890s.

While the minimum wage is designed to guarantee a basic living standard for low-wage workers, supply and demand models in economics suggest that raising the minimum wage may result in some loss of employment. Empirically, however, there is no consensus over whether raising the minimum wage does in fact lead to higher unemployment rates.

Causally this is a tough question to answer because countries or localities don’t want to participate in a randomized experiment on minimum wage for the sake of research. Thus, we only have observational data at our disposal.

Imagine we gave you data for the US. The data is broken down at the state level and includes a variable indicating whether a state passed a minimum wage increase (MWI). It also includes a variable for the employment rate in each state.

At this point, we don’t have to tell you why a simple comparison of employment rates between states that pass MWI and those that don’t will not work. States that pass an MWI may be different from the states that don’t in unobservable ways, for instance, the political climate in the state. So, for the thousandth time, we have a causal issue 😫

Card and Krueger, two famous labor economists, didn’t give up. They simply thought this was a great opportunity to put DiD to work. Their paper is considered a classic example of the DiD method in action.

So what exactly did they do?

Their study begins in New Jersey where in 1992 the state-wide minimum wage was raised from $4.25 an hour to$5.05 an hour. This may seem like a modest increase in absolute terms but think about it in percentage terms. This was an 18 percent increase! In neighboring Pennsylvania, there was no hike in the minimum wage. Card and Krueger exploited this difference. They collected data from individual businesses that employed minimum wage workers in each state and compared what happened in Jersey to what happened in Pennsylvania before and after the MWI in New Jersey was introduced. DiD relies on only two points in time as this example shows (a before and an after).

New Jersey received the treatment (passed an MWI law) and Pennsylvania didn’t. Card and Krueger lacked the potential outcome under no treatment for New Jersey and the potential outcome under treatment for Pennsylvania. Jersey is Jersey and Pennsylvania is Pennsylvania. We’ve already established that there’s no use comparing employment in one state to the other.

We’ll denote the employment rate in New jersey as $Y_{\text{NJ}}$, and the employment rate in Pennsylvania as $Y_{\text{PA}}$. Employment in each state relies on a number of factors some of which are state-specific, and these factors may be observed or unobserved.

In the table above, $Y_{\text{MWI}}$ captures the employment effects due to the MWI. We only include this for Jersey, since Pennsylvania didn’t pass an MWI. Note that $Y_{\text{MWI}}$ can be a negative number if the MWI leads to a decrease in the employment rate.

If we compare the outcomes in each state (the employment rates), we get $Y_{\text{NJ}}+Y_{\text{MWI}}-Y_{\text{PA}}$. Note that this is what we previously called the naive treatment effect and it’s biased. The true causal effect that we’re after would be $Y_{\text{MWI}}$ because it’s the employment rate solely due to the treatment.

We are now going to introduce the time dimension!

Let’s only look at Jersey. If we observe New Jersey’s employment both before and after passing the MWI, can we attribute the difference to the passage of the MWI? The short answer is no!

During the period of study, other things could have changed that affected the employment rate in either or both states - a small economic recession, for example. So really we need to include $Y_{\text{Time, NJ}}$ to reflect changes in Jersey’s employment rate that result from passage of, and similarly, we need to add $Y_{\text{Time, PA}}$ to reflect the same for Pennsylvania.

If we want to show this time variable using a DAG, this is how we proceed:

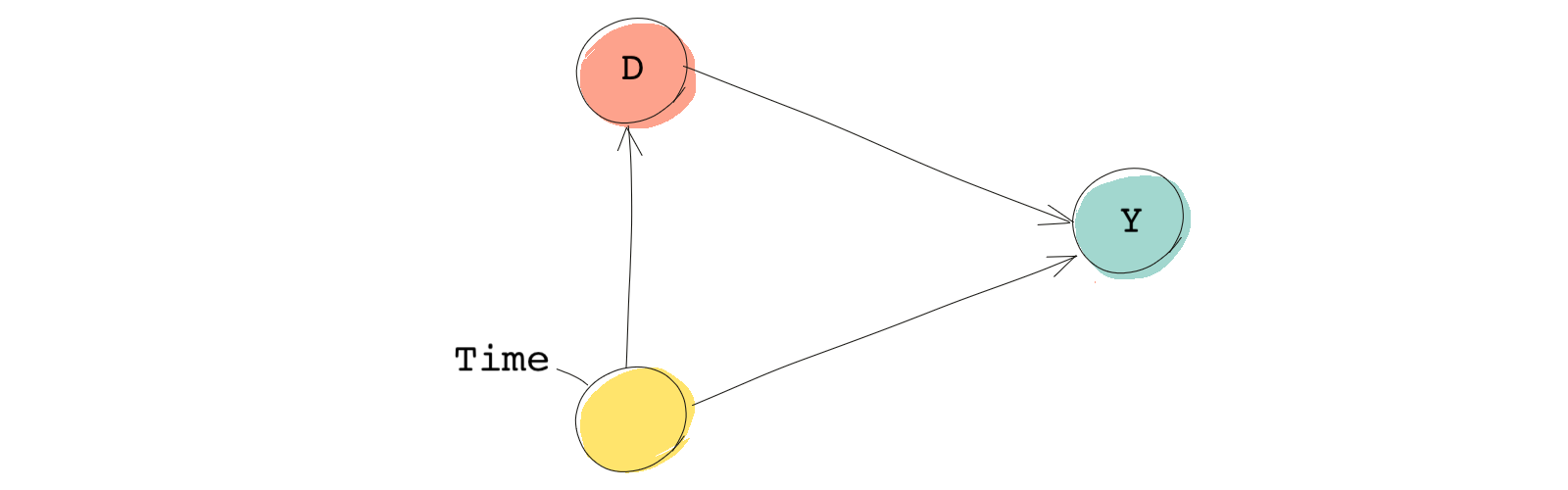
Time clearly affects the outcome. But it also determines the treatment status as well. Because if we’re in the pre-treatment period, then subjects don’t receive treatment and if we’re in the post-treatment period, subjects (those in the treatment group) receive treatment.

As a result we have a backdoor!

Can we simply control for time and estimate the unbiased treatment effect? We would certainly have a variable in our data variable indicating the time period, but the answer is no, again!

Treatment status and time are perfectly correlated, so if we control for time, we are effectively controlling for the treatment itself. If we control for the treatment, we won’t find its causal effect. 🤷🏽‍♂️

Let’s keep trying.

If we compare Jersey to itself, before and after treatment, the change in the employment rate is:

• $Y_{\text{MWI}} + Y_{\text{Time, NJ}}$.

If we compare Pennsylvania to itself before and after Jersey’s MWI we get:

• $Y_{\text{Time, PA}}$.

Neither of these is the treatment effect we are after. These are only a comparison of the post-MWI employment rate to the pre-MWI employment rate in each state. We’re after $Y_{\text{MWI}}$.

Now, let’s look at the differences in differences between each state:

• $Y_{\text{MWI}} + Y_{\text{Time, NJ}}-Y_{\text{Time, PA}}$

We’re still not quite there yet, but what if we assume the time effect in both states are the same, i.e., $Y_{\text{Time, NJ}} = Y_{\text{Time, PA}}$? Does this assumption help us find the treatment effect we’re after? Yes!

The DiD method is called difference-in-differences because the treatment effect can be calculated by:

1. Estimating the before-after difference in the outcome for the treatment group (Jersey here): $Y_{\text{MWI}} + Y_{\text{Time, NJ}}$
2. Estimating the before-after difference in the outcome for the control group (Pennsylvania here): $Y_{\text{Time, PA}}$
3. Calculating the difference between the terms in steps 1 and 2 above (the differences in differences): $Y_{\text{MWI}} + Y_{\text{Time, NJ}} - Y_{\text{Time, PA}}$.
4. Assuming that $Y_{\text{Time, NJ}} = Y_{\text{Time, PA}}$. With this assumption, the estimated effect calculated in 3 simplifies down to $Y_{\text{MWI}}$, the treatment effect due to the MWI in Jersey.

Notice that the end result is a causal effect $Y_{\text{MWI}}$, which is isolated from any of the other differences between the states or between the two time periods. The beauty of DiD is that under the assumption we made, any difference between the control group and the treatment group vanishes because we compare each group to themselves.

Similar to the synthetic control method, DiD aims at balancing pre-intervention trends in the outcome variables. Unlike synthetic control, however, DiD doesn’t depend on the treatment and control groups being similar across covariates. Rather, we need to assume that both change to the same degree over time. This is the key assumption of DiD. It’s a strong assumption.

DiD assumes that, everything else being equal, the two units (treated and control) would have followed parallel trends over time in the absence of treatment. This assumption is called the parallel-trends assumption. The following graph shows the assumption in the context of our minimum wage example.

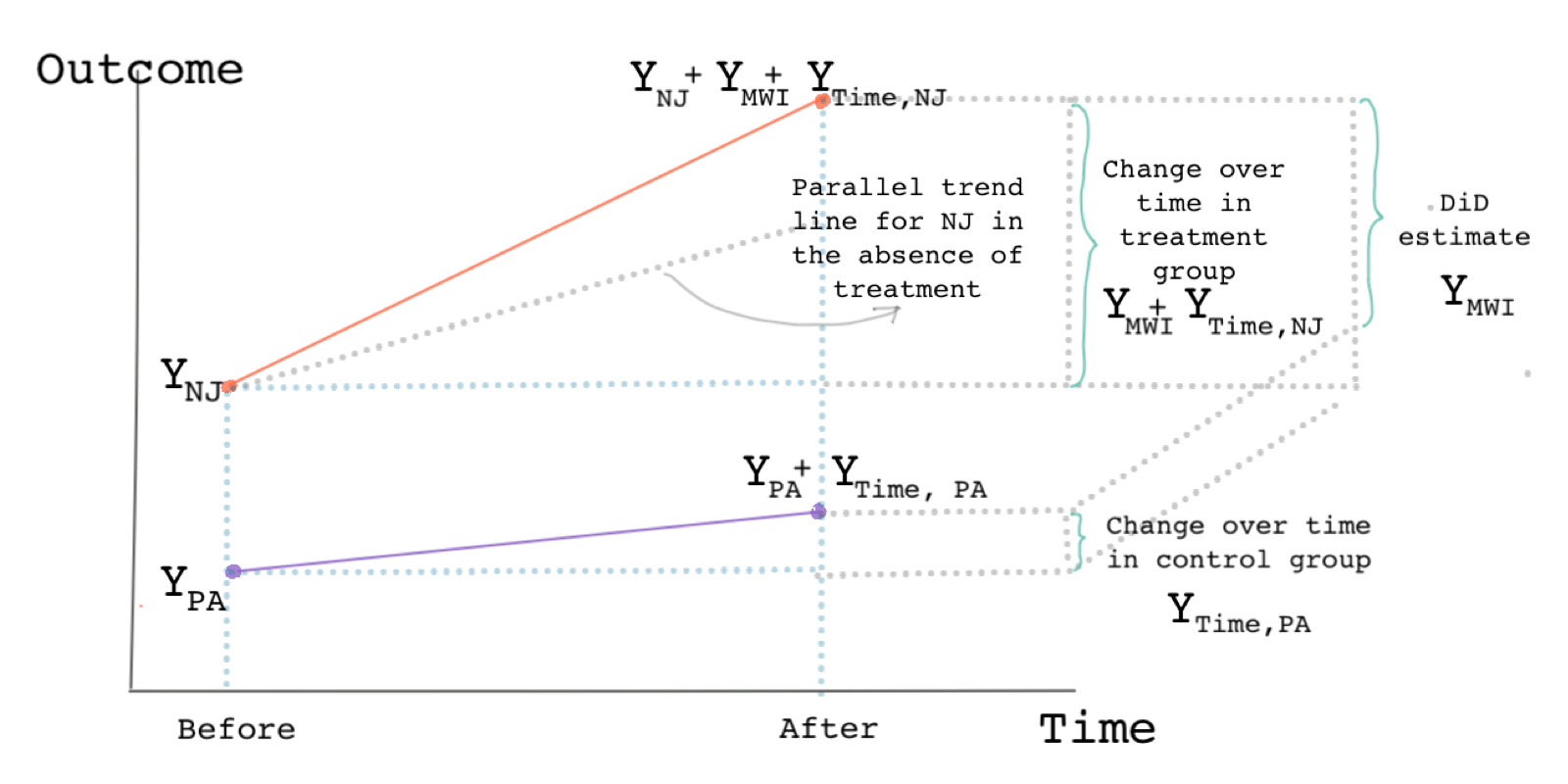
The dotted line shows the parallel-trends assumption.

What makes the DiD method attractive is that by taking the pre- and post-treatment differences we eliminate the individual effects (selection bias) and by taking the treatment-control differences we eliminate the time effects. Therefore, we eliminate the influence of unobserved covariates almost entirely.

Now that we know how to work with DiD in a simple one-treatment-one-control and two-time-period case, let’s estimate the causal effect in our example. Card and Krueger found the following numbers:

The numbers in the table above show full-time employment in both states before and after the MWI. From here estimating the treatment effect should be easy.

• The before-after difference in the outcome for the treatment group (Jersey here) is $0.59$. Note that this number is in terms of average employment per store. Therefore, as a result of the MWI, the average employment per store increased by 0.59 employees.
• The before-after difference in the outcome for the control group (Pennsylvania here) is $-2.16$
• The difference-in-differences causal estimate is then the difference of the two which is $0.59-(-2.16) = 2.75$

This means the estimated causal effect of the minimum wage hike in New Jersey was a 2.75 increase in the employment rate.

The publication of the paper marked the beginning of a significant change in the attitude of many economists towards minimum wage laws. This helps demonstrate the influence of causal inference-based research since this paper empirically claimed something that contradicted economic theory.

On the other hand, there are important considerations to highlight from the critics of the paper as well. They had two major complaints:

1. The selection of the before-and-after points: The NJ MWI went into effect in 1992, but it was announced two years prior. Hence, employers in NJ had roughly two-years to adjust their employment behavior and the comparison. If employers did in fact change their behavior in advance of the policy implementation, the comparison of employment just before and after 1992 may not be as insightful as the authors hoped.
2. The second critique is about something we learn more about in the next lesson. This critique is about the parallel-trends assumption. Both states did in fact experience a small recession during the period of study. Even if this recession impacted employers in NJ and PA in similar ways, the response of employees in each region may have been different. There is some evidence that employees in Pennsylvania let workers go, while employers in New Jersey increased their menu prices (the businesses Card and Krueger looked at were fast-food restaurants).

A more general representation

In the example above, we only looked at two states. A more general approach to DiD includes more treatment and control subjects. Below, $i$ represents subject $i$, $t$ represents the post-treatment time period and $t'$ represents the pre-treatment time period.

• We estimate the average before-and-after difference in outcomes for the treatment group: $E({Y_{it}}-{Y_{it'}} | D_{it} = 1)$
• We estimate the average before-and-after difference in the outcome for the control group: $E({Y_{it}}-{Y_{it'}} | D_{it} = 0)$
• We then calculate the difference-in-differences, assuming the parallel-trend assumption holds.

From what you’ve already seen, estimating DiD is very easy and boils down to taking differences. We can also use a regression model for estimating DiD causal effects. This is especially useful when we have many treatment and many control units. To do this, we need to transform our dataset such that:

• We have a variable indicating whether the observation is from before or after implementing the treatment (let’s call it $Post$ which is 1 if the observation refers to post-treatment and 0 otherwise)
• We have a variable indicating whether the observation is in the treated group or the control group (let’s call this $D$ which is 1 if the subject in in the treatment group and 0 otherwise)
• We have a variable indicating the interaction of the two variables above (simply $D \times Post$)

Once we have that, we can use the following regression model to estimate the DiD effect:

Here, $i$ refers to unit $i$, and $t$ refers to time $t$. The error terms eventually cancel out in our calculations, so we can ignore them. We will see that $\delta$ is the DiD estimator.

How does this regression give us the same DiD treatment effect we estimated by simply taking the differences?

In our example, the treated unit was New Jersey. Therefore, we can replace the treatment binary variable with a binary variable indicating whether the observation is Jersey or not. To be consistent, we can replace the variable $Post$ with $Time$, which is what we initially used. The resulting regression is:

How do we find the outcomes for NJ and PA before and after the MWI?

In New Jersey:

• Before the treatment was imposed the average employment per store is: $\beta_0 + \beta_1$
• After the treatment was imposed the average employment per store is: $\beta_0 + \beta_1 + \beta_2 + \delta$
• Therefore, the before-and-after difference in treatment outcomes is then $\beta_2 + \delta$

In Pennsylvania:

• Before the treatment was imposed the average employment per store is: $\beta_0$
• After the treatment was imposed the average employment per store is: $\beta_0 + \beta_2$
• The before-and-after difference in treatment outcomes is $\beta_2$

Finally, the difference-in-differences: $\beta_2 + \delta - \beta_2 = \delta$

So $\delta$ is indeed the difference-in-differences estimator we’re after.