What is a good instrument?

In the previous lesson, we learned about the IV approach and the assumptions needed to identify a good instrument. We saw that for a variable to qualify as an IV, it has to satisfy the relevance assumption, the exclusion restriction, and the no-confounding assumption. Once we have an IV at our disposal, it also has to satisfy the monotonicity (no-defier) assumption as well.

In reality, it’s hard to find instruments that satisfy all these assumptions. Angrist and Krueger, two famous empirical economists who popularized the use of instruments in economics, say that the best instruments come from deep subject matter knowledge. To understand the process of finding an instrument, let’s start with the perfect case of an instrument. The coin flip ☝️

A coin flip is an ideal instrument

Flipping a coin to determine treatment assignment is a great example of an instrument. You can always return to this example to mentally compare how your IV measures up.

Imagine, that a coin flip determines our treatment: enrollment in a job training program. The outcome variable of interest is future earnings. Our coin flip variable takes a value of Heads (H) or Tails (T), which we could also denote as 0 (heads) or 1 (tails). It affects the treatment (because it determines who receives the training program and who doesn’t), and it is only associated with our outcome variable through the treatment. Lastly, the coin flip doesn’t share any causes with the outcome.

If you can further assume monotonicity in your data, all necessary conditions for a valid IV have been met. The following DAG summarizes the causal relationships.

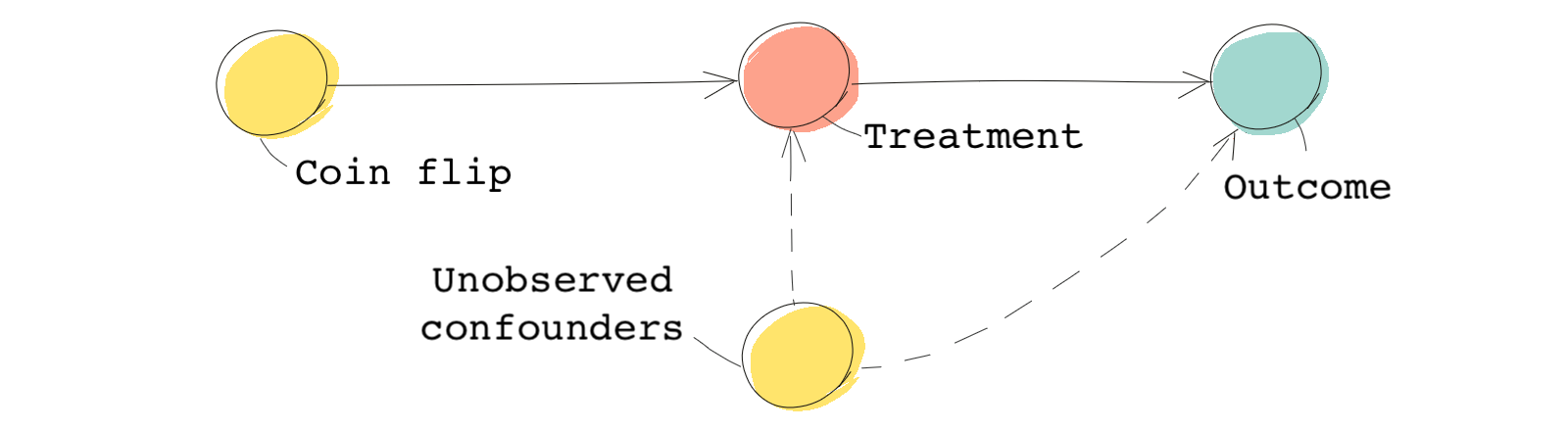
In encouragement designs, too, we can think of encouragement as an instrument. Encouragement affects (strongly or weakly) who receives the treatment, and it is not directly associated with the outcome nor does it share common causes with the outcome. As a matter of fact, a good IV is usually thought to resemble a strong encouragement.

In practice, we can check the relevance assumption (association between the IV and treatment variable) empirically. We can’t really test the exclusion restriction empirically, especially if subjects are not blinded. Checking to see whether the exclusion restriction holds requires intuition and knowledge of the subject matter. Unfortunately, it’s very common that the exclusion restriction is violated 😞

In what follows, we go over some examples of how IV’s have been used in practice.

Example one: Does college affect wages?

The effect of college education on wages has been a key research area in labor economics. Does college increase wages, and if so, by how much? This is a tricky causal question to answer with many potential confounders, many of which are unobservable. Think about motivation as a confounder. It affects who goes to college; it affects wages; it’s pretty difficult, if not impossible, to measure.

Instruments offer a solution. In thinking about this very problem, David Card wondered what factors encourage treatment (going to college) and satisfy the rest of the assumptions for IVs. The instrument he came up with in this 1995 paper was proximity to college.

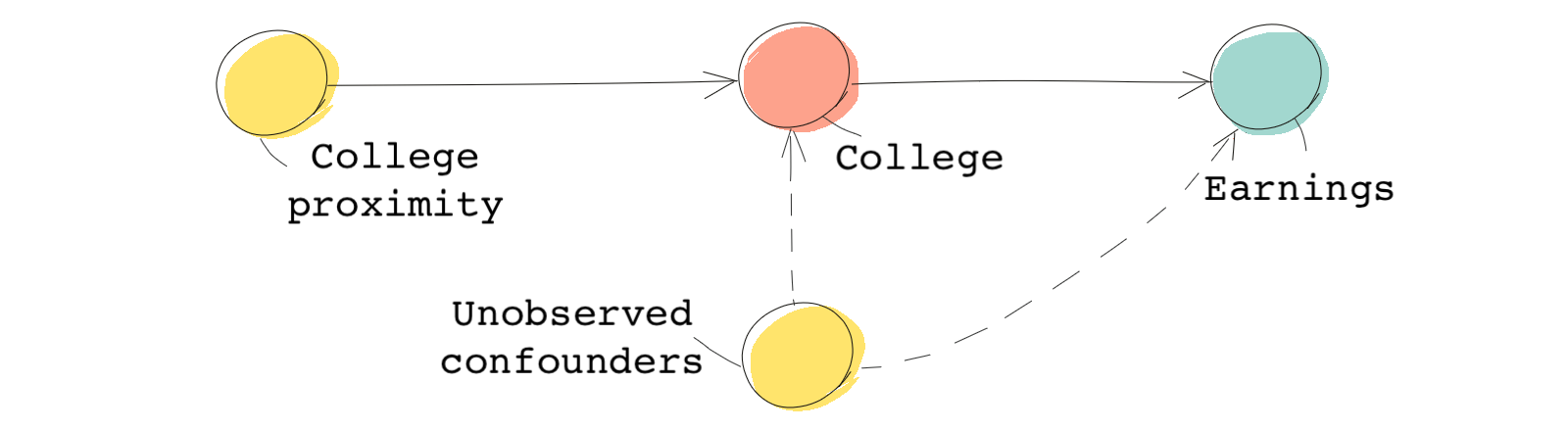
Here are Card’s assumptions. College proximity isn’t associated with wages, but it directly affects who goes to college. You can think of college proximity as an incentive (encouragement) for going to college. He thought this instrument satisfied the no-confounding assumption as well. Do you think these are valid assumptions?

Example two: Does smoking affect a child’s birth weight?

Here the causal question is: If a parent smokes, does that affect their children’s birth weight? We can’t run a randomized experiment for obvious reasons, and there are plenty of plausible confounders. Smoking could be correlated with other health factors that also affect birth weights. For instance, alcohol consumption might be correlated with smoking and also with the birth weight of the child.

Is there a valid instrument we could use to help answer this question? Evans and Ringel thought so. Here’s a link to their 1997 paper.

You might be surprised to learn that cigarette prices vary quite a bit from state to state in the United States. Different states have different tax rates on cigarettes, which translates into differences in price.

Now let’s evaluate this instrument based on the assumptions. Does the instrument work as an encouragement? When cigarettes are cheaper, individuals are encouraged to buy more cigarettes and smoke more. So, yes. Should we expect cigarette prices to affect the birth weights of babies other than through the smoking behaviors of their parents? There doesn’t seem to be any reason to think it would. Finally, are there any common causes between cigarette prices and birth weights? You’d be hard-pressed to come up with one.

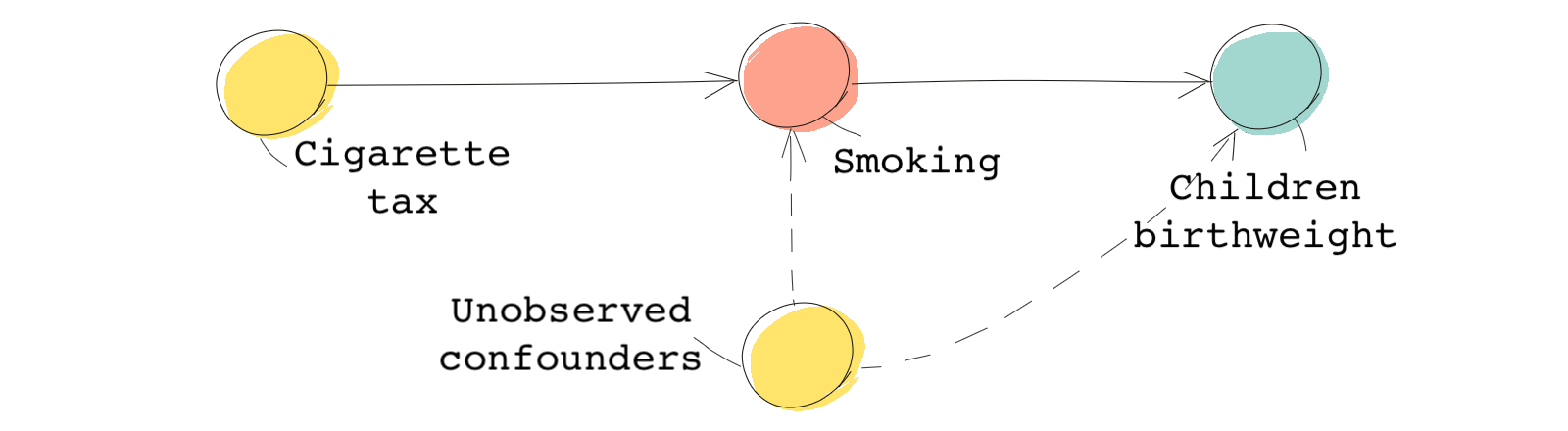
This seems to satisfy the IV assumptions, and following in the footsteps of Evans and Ringel, we should be able to find the LATE estimate.

Example three: Does economic growth affect conflicts?

This last example is simple, but it has a surprising IV, and it’s an actual example in development economics from a paper by Miguel, Satyanath, and Sergenti (2004). The authors were interested in the causal effect of economic growth on civil conflict. Even after controlling for measurable confounders such as population, oil exports, democracy, and religion, other unobservable confounders seemed to remain.

The unexpected instrumental variable the authors landed on? Rainfall 😲

Now, how on earth does rainfall work here? The authors’ rationale is this. Rainfall is a good predictor of agricultural development, which affects economic growth. Through this association with treatment variable, the relevance assumption is met.

Next, the authors assumed no other causal paths from rainfall to conflict. This, they admitted, could be refuted, and if you were critiquing their paper you might challenge their assumption on this point. It could be the case that conflict and civil unrest are linked through channels such as tax revenue, road networks, and heatwaves. As long as those factors are observable, however, the authors could control for them and block the confounding paths.

In general, rainfall is somewhat random in nature and thus resembles a coin flip. You could also view it as an encouragement for economic growth.

The following DAG summarizes the causal relationships in this example. $C$ is a set of variables that shape the potential path between the instrument and the outcome, therefore, violating the exclusion restriction. However, as we said, if you can control for these variables and block the path, they are not problematic. $U$ represents the set of unobserved confounders between the treatment and outcome.

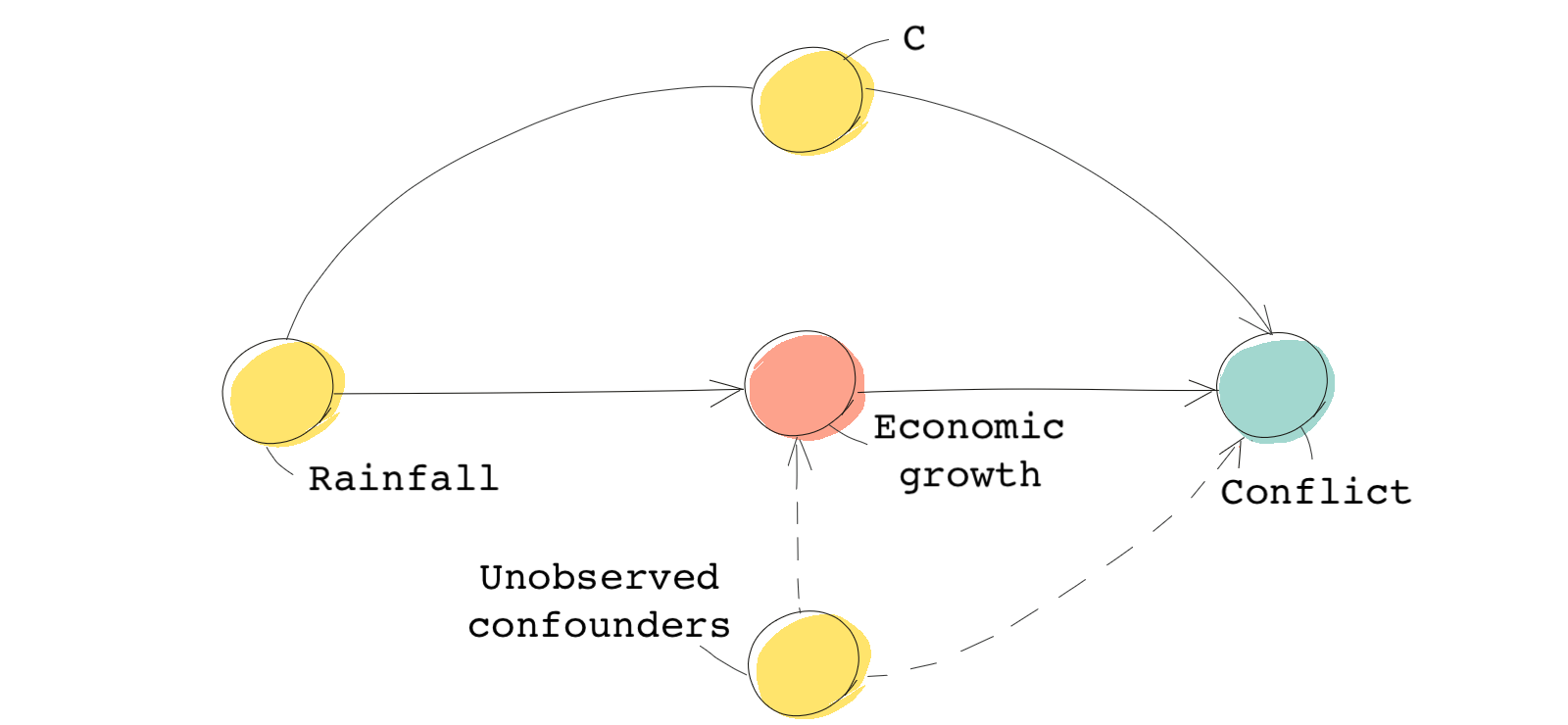
If all C’s are observable and this DAG is accurate, rainfall works as an instrument and can be used to estimate the local average treatment effect (LATE) among compliers.

Practice

For this example, what are the compliers?

Countries where it rains a lot.

Countries where growth has nothing to with rainfall.

Countries in which higher rainfall causes less growth and lower rainfall causes more growth.

Countries in which higher rainfall causes more growth and lower rainfall causes less growth